2. Arbres et arborescences▲
Il existe deux approches classiques de la notion d'arbre : le point de vue de la théorie des graphes, où un arbre est une variété d'espace topologique et le point de vue des structures de données, où un arbre - ou plutôt une arborescence - est une structure que l'on donne à un ensemble d'informations.
2-1. Arbres▲
Un arbre est un graphe(3) non orienté G = ( S , A ) qui vérifie les propriétés équivalentes suivantes :
- G est connexe minimal (si on lui enlève une arête il n'est plus connexe) ;
- G est acyclique maximal (si on lui ajoute une arête on crée un cycle) ;
- | A | = | S | - 1 et G est connexe ou acyclique ;
- deux sommets quelconques de G sont reliés par un unique chemin élémentaire.
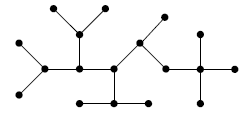
Un arbre enraciné est un arbre dans lequel un des sommets, appelé la racine, est distingué.
Soit G un arbre enraciné de racine r et x un sommet de G. Un sommet y appartenant au chemin unique allant de r à x est appelé ancêtre de x, et x est alors appelé descendant de y. Si (y, x) est le dernier arc du chemin joignant r à x, on dit que y est le père de x et que x est le fils de y. La racine n'a pas de père. Si deux sommets ont le même père, on dit qu'ils sont frères. On appelle sous-arbre de racine x le sous-arbre de G composé de x et ses descendants.
2-2. Arborescences▲
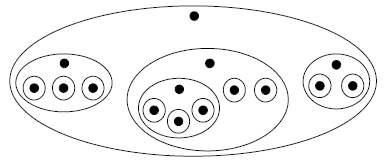
Une arborescence est un ensemble fini non vide A muni de la structure suivante :
- il existe un élément distingué, appelé la racine de A ;
- l'ensemble des autres éléments de A, s'il n'est pas vide, est partitionné(4) en une famille de sous-ensembles qui sont des arborescences.
2-2-1. Jargon sur les arbres▲
ABUS DE LANGAGE. Il arrive rarement que l'on ait à traiter, dans le même discours, des arbres et des arborescences. On se permet donc d'employer le même vocabulaire, celui des arbres, pour travailler sur les arbres et sur les arborescences ; en principe, le contexte indique toujours de quoi il s'agit.
Nous pratiquerons ici cet abus de langage et nous dirons désormais arbre pour arborescence.
Sous-arbre immédiat. Soit A un arbre de racine r. Par définition, l'ensemble A - { r } est partitionné en une famille d'arbres ; ces derniers sont appelés les sous-arbres immédiats de A.
Sous-arbre. B est un sous-arbre de A si : B est un sous-arbre immédiat de A, ou s'il existe C, sous-arbre immédiat de A, tel que B soit un sous-arbre de C.
Nœud. Les éléments de A sont appelés nœuds. Chaque nœud est racine d'un sous-arbre de A (pour s'en convaincre il suffit d'appliquer récursivement la définition d'arbre). Inversement, chaque sous-arbre possède une racine. Il y a donc une bijection entre les nœuds et les sous-arbres d'un arbre.
Ancêtre, descendant. Soit X un sous-arbre de A de racine x et soit y un élément d'un sous-arbre de X. On dit que x est un ancêtre de y et que y est un descendant de x.
Père, fils, frère. Soit X un sous-arbre de A de racine x et soit y la racine d'un sous-arbre immédiat de X. On dit que x est le père de y, et que y est un fils de x. Parler de « un arbre et ses sous-arbres immédiats » revient donc à parler de « un nœud et ses fils ». Entre eux, les fils d'un nœud sont dits frères.
Représentation par un graphe orienté. La représentation habituelle des arbres consiste à représenter les nœuds, puis à relier par des flèches, implicitement orientées du haut vers le bas, chaque nœud à ses fils :
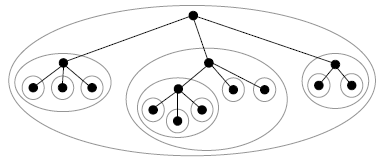
Feuilles. Un nœud qui n'a pas de fils est appelé nœud externe ou feuille. Un nœud qui n'est pas une feuille est un nœud interne.
Degré. Le nombre de fils d'un nœud est le degré de ce nœud. Un nœud de degré 0 est donc une feuille.
Profondeur. Soit x un nœud d'un arbre A. La profondeur de x dans A est la longueur (c.-à-d. le nombre d'arcs) du chemin allant de la racine de A à x.
Hauteur. La hauteur d'un arbre A est le maximum des profondeurs de ses nœuds.
Arbre ordonné. S'il existe une relation d'ordre définie sur les fils de chaque nœud, alors on dit que l'arbre est ordonné. Les arbres sont souvent ordonnés, parfois involontairement : comment nommer, dessiner, etc. un arbre sans l'ordonner ?
2-2-2. Implantation des arbres▲
En vue de les implanter dans les programmes, on peut formaliser la définition des arbres de la manière suivante :
- Soit X un ensemble donné. Un arbre dont les nœuds portent des éléments de X est un couple ( i , E ) constitué d'un élément i ∈ X et d'un ensemble fini E, éventuellement vide, d'arbres dont les nœuds portent des éléments de X.
Comme on l'a dit, on a beaucoup de mal à empêcher les arbres d'être ordonnés ; en pratique un ordre existe toujours entre les fils d'un nœud. Pour ce que nous avons à en faire ici, nous ne perdons pas grand-chose en remplaçant la définition précédente par la définition plus restrictive suivante :
- Soit X un ensemble donné. Un arbre dont les nœuds portent des éléments de X est un couple ( i , ( A1, A2… An ) ) constitué d'un élément i ∈ X et d'une suite finie ( A1, A2… An ), éventuellement vide, d'arbres dont les nœuds portent des éléments de X.
L'implantation des arbres découle de cette définition :
- la suite ( A1, A2… An ) est représentée par une liste chaînée d'arbres ;
- un arbre est représenté comme un couple (info, liste-de-fils)
Si on était tout à fait rigoureux, on devrait donc déclarer : d'un côté, un arbre comme un couple :
typedef struct arbre
{
OBJET info;
LISTE_D_ARBRES fils;
} ARBRE;et, d'un autre côté, une liste d'arbres, comme nous savons déjà le faire :
typedef struct maillon
{
ARBRE sousArbre;
struct maillon *frere;
} *LISTE_D_ARBRES;En réalité, on se contente d'un peu moins de rigueur et on fait l'unique définition :
typedef struct noeud
{
OBJET info;
struct noeud *fils;
struct noeud *frere;
} NOEUD, *POINTEUR;qui correspond à :
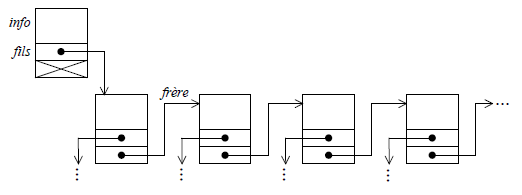
C'est moins rigoureux parce qu'on met sur le même plan les fils et les frères, ce qui n'a pas de justification dans la notion d'arbre que nous avons donnée.
À RETENIR
Dans le cas général (la situation est différente dans le cas des arbres binaires), l'arbre dont la structure « logique » est celle de la figure 5 (a) s'implante comme le montre la figure 5 (b) :
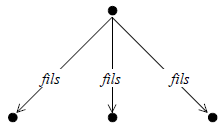 |
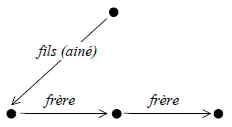 |
2-3. Arbres binaires▲
Dans les arbres binaires, chaque nœud a au plus deux fils. Bien sûr, on peut les voir comme un cas particulier des arbres quelconques, mais dans beaucoup de domaines on préfère la définition spécifique suivante, qui est à rapprocher de la définition des listes du chapitre 1, section 1.2.4Faut-il utiliser un tableau ou une liste chaînée ?.
DÉFINITION
Soit X un ensemble donné. Un arbre binaire portant des éléments de X est : un symbole conventionnel, appelé arbre vide, ou un triplet ( i , G, D ) où i ∈ X et où G et D sont des arbres binaires portant des éléments de X.
L'implantation usuelle des arbres binaires découle de cette définition :
typedef struct noeud
{
OBJET info;
struct noeud *gauche, *droite;
} NOEUD, *POINTEUR;Par exemple, l'expression arithmétique 3 x (a + 5) pourrait être représentée par l'arbre binaire.
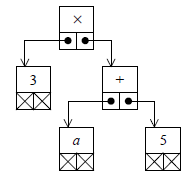
2-4. Parcours des arbres▲
On appelle parcours d'un arbre A le travail qui consiste à effectuer un certain traitement, dépendant de l'application particulière considérée, sur l'information portée par chaque nœud de A.
C'est sans doute le meilleur exemple d'algorithme récursif que l'on puisse trouver. Partant du problème « parcourir l'arbre A = ( i , ( A1 … An ) ) », on obtient :
- un problème simple : « traiter i » ;
- n problèmes analogues au problème initial : « parcourir A1 »… « parcourir An ».
Un point reste à régler, qui dépend de l'application particulière considérée : dans quel ordre doit-on faire les n + 1 opérations mentionnées ci-dessus ?
2-4-1. Parcours des arbres binaires▲
Dans le cas des arbres binaires les trois manières possibles d'arranger ce parcours sont fréquemment utilisées et ont fait l'objet de dénominations spécifiques : le parcours en préordre, le parcours en in-ordre et le parcours en postordre, définis respectivement par le fait que chaque nœud est traité avant, entre ou après les parcours de ses deux fils.
Ainsi, le parcours en préordre peut se programmer :
void parcours(POINTEUR arbre)
{
if (arbre != NULL)
{
EXPLOITER(arbre->info);
parcours(arbre->gauche);
parcours(arbre->droite);
}
}Les fonctions qui implantent les deux autres parcours ne diffèrent de celle-ci que par la position de l'appel d'EXPLOITER relativement aux deux appels de parcours.
À titre d'exemple, considérons encore le codage par un arbre binaire de l'expression 3 × (a + 5), et supposons que la fonction EXPLOITER se réduise à l'affichage du champ info de chaque nœud. L'effet du parcours de l'arbre sera donc un certain affichage de l'expression. On obtient :
- dans le parcours en in-ordre : 3 × a + 5 (notation infixée - et ambiguë !) ;
- dans le parcours en préordre : × 3 + a 5 (notation « polonaise ») ;
- dans le parcours en postordre : 3 a 5 + × (notation « polonaise inversée »).
2-4-2. Parcours d'un arbre quelconque▲
On utilise souvent le parcours qui correspondrait au préordre :
void parcours(POINTEUR arbre)
{
POINTEUR p;
EXPLOITER(arbre->info);
for (p = arbre->fils; p != NULL; p = p->frere)
parcours(p);
}Notez que ce programme est juste parce que, avec notre définition, un arbre (non binaire) ne peut pas être vide.
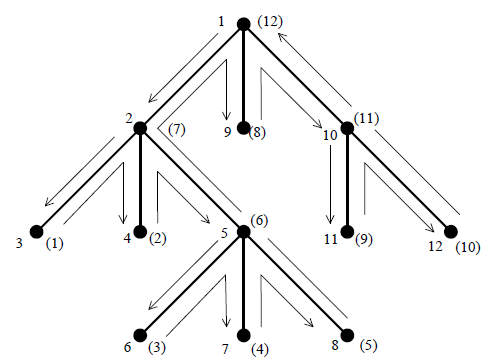
La figure 7 montre le travail de la fonction parcours, comme l'itinéraire d'une bestiole se promenant sur l'arbre. Les flèches vers le bas représentent les appels que la fonction parcours fait d'elle-même ; on appelle cela la « descente aux fils ». Chaque appel parcours(p) provoque le parcours du sous-arbre ayant p pour racine. Lorsque ce parcours est terminé, le contrôle revient à la fonction qui a fait l'appel de parcours. Ce retour est symbolisé par la partie remontante des flèches ; vu du côté du fils, on appelle cela la « remontée au père ».
Les nombres écrits à gauche de chaque nœud expriment la chronologie de leur exploitation dans le cas du parcours en préordre. Les nombres écrits entre parenthèses, à droite de chaque nœud, correspondent au cas du postordre.
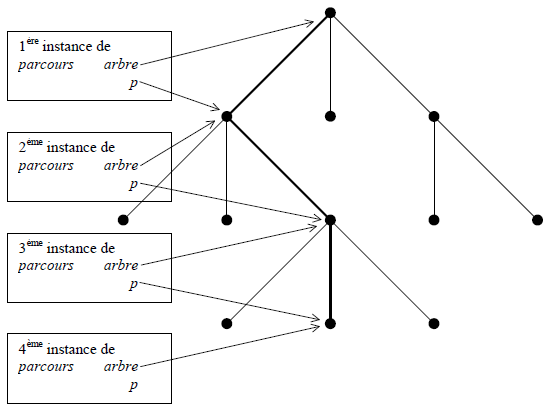
La figure 8 montre un moment du parcours de l'arbre précédent : celui où le sommet marqué 7 - (4) va être exploité. Quatre instances de la fonction parcours sont actives (quatre générations distinctes des variables arbre et p existent donc en même temps, empilées les unes au-dessus des autres) : dans la première, la boucle for en est à son début ; C'est-à-dire la variable p correspondante pointe le premier fils de arbre ; dans la deuxième instance, la boucle for en est à son dernier tour, dans la troisième, elle en est au milieu. Dans la quatrième instance, la boucle for ne démarrera même pas.
VARIANTE
Dans l'algorithme de parcours d'un arbre il y a un aspect naturellement récursif, la descente au fils, et un aspect naturellement itératif, le parcours de la liste de frères. Or, nous l'avons vu, une liste chaînée peut aussi être parcourue selon une fonction récursive. On peut en déduire une fonction de parcours d'arbre doublement récursive, qui utilise la récursivité pour la descente aux fils et aussi pour le parcours de la liste des frères. Ce qui donne le programme correct et apparemment très élégant suivant :
void parcours(POINTEUR arbre)
{
if (arbre != NULL)
{
EXPLOITER(arbre->info);
parcours(arbre->fils);
parcours(arbre->frere);
}
}À notre avis, ce programme est moins satisfaisant pour l'esprit que la version précédemment donnée, aussi bien du point de vue stylistique, car on met sur le même plan les fils et les frères, que de point de vue de l'efficacité, car on programme récursivement un traitement qui aurait pu être programmé aussi simplement de manière itérative.
2-5. Applications▲
2-5-1. Arbre lexicographique (codage en parties communes)▲
Proposons-nous d'implanter une sorte de dictionnaire, c'est-à-dire une structure de données servant à mémoriser un ensemble de mots(5). Le dispositif réalisé doit permettre de rechercher et au besoin d'insérer des mots au fur et à mesure des besoins. On supposera qu'aucun mot ne se répète dans le dictionnaire, et que l'échec de la recherche d'un mot doit provoquer automatiquement son insertion dans le dictionnaire. Enfin, nous souhaitons disposer d'une fonction qui affiche la liste par ordre alphabétique de tous les mots contenus dans le dictionnaire.
Ce qui va suivre sera fait avec des chaînes (c'est-à-dire des tableaux) de caractères, mais s'adapte facilement à des tableaux de n'importe quelle sorte d'objets appartenant à un ensemble totalement ordonné. Le principe du dispositif consiste à maintenir un arbre, dont les nœuds ont pour informations spécifiques des caractères et sont définis de la manière suivante :
- la racine est conventionnelle et ne porte aucune information significative ;
- les fils de la racine sont des nœuds qui portent les premières lettres des mots, rangées par ordre alphabétique ;
- soit r un des fils de la racine, c la lettre qu'il porte. Les fils de r sont des nœuds qui portent les deuxièmes lettres, rangées par ordre alphabétique, des mots commençant par c ;
- plus généralement, soit r0r1r2…rn un chemin depuis la racine (r0 est la racine), c1c2…cn les lettres respectivement rangées dans ces nœuds. Les fils de rn sont des nœuds qui portent les (n+1)e lettres, rangées par ordre alphabétique, des mots commençant par c1c2…cn.
Par exemple, la figure 9 montre l'arbre correspondant aux mots : main, mais, mal, mâle, mon, son, sono, sons, sont :
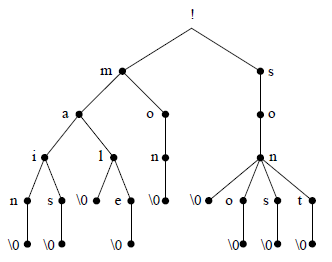
On notera que les mots ne sont pas représentés par les nœuds, mais par les chemins depuis la racine. L'appellation « arbre lexicographique » est tout à fait justifiée : c'est l'arbre qui incarne l'ordre lexicographique, un nœud pris isolément n'a aucune signification.
Chaque mot se termine par un caractère spécial (en C, nous utiliserons le '\0' qui se trouve à la fin de chaque chaîne) qui :
- caractérise le mot : c'est le seul caractère dont on est sûr qu'il n'y en a qu'un par mot(6),
- doit être inférieur aux autres lettres (afin que "abc" soit inférieur à "abcd").
Voici le programme. Une fois de plus, le problème se ramène à celui de l'insertion dans une liste triée. Déclarations :
typedef struct noeud {
char info;
struct noeud *fils, *frere;
} NOEUD, *PTR;
PTR noeud(char info, PTR fils, PTR frere) {
PTR p = malloc(sizeof(NOEUD));
assert(p != NULL);
p->info = info;
p->fils = fils;
p->frere = frere;
return p;
}La fonction de recherche-insertion rend 0 lorsque le mot recherché n'existait pas dans l'arbre (il y a donc eu création d'au moins un nœud pour un caractère), 1 lorsque le mot était déjà dans l'arbre (aucune création) :
int rechinsertion(char mot[], PTR ancetre) {
PTR pr, pc;
int i;
/* à chaque tour de cette boucle on recherche le caractère */
/* mot[i] parmi les fils du nœud pointé par ancetre */
for(i = 0; ; i++) {
pr = NULL;
pc = ancetre->fils;
while (pc != NULL && pc->info < mot[i]) {
pr = pc;
pc = pc->frere;
}
if (pc != NULL && pc->info == mot[i]) {
if (mot[i] == '\0')
return 1; /* le mot existait */
ancetre = pc;
}
else {
pc = noeud(mot[i], NULL, pc);
if (pr != NULL)
pr->frere = pc;
else
ancetre->fils = pc;
while (mot[i] != '\0') {
pc->fils = noeud(mot[++i], NULL, NULL);
pc = pc->fils;
}
return 0; /* le mot est nouveau */
}
}
}Affichage, dans l'ordre lexicographique, des mots de l'arbre :
static struct {
char t[80];
int n;
} pile;
void parcours(PTR arbre) {
PTR p;
pile.t[pile.n++] = arbre->info;
if (arbre->info == '\0')
printf("%s\n", pile.t + 1);
else
for (p = arbre->fils; p != NULL; p = p->frere)
parcours(p);
pile.n--;
}Petit programme pour essayer tout cela :
main() {
char mot[80];
int i;
PTR racine = noeud('!', NULL, NULL);
while (gets(mot) != NULL)
printf("le mot %s est %s\n", mot,
rechinsertion(mot, racine) ? "ancien" : "nouveau");
pile.n = 0;
parcours(racine);
}2-5-2. Sauvegarde et restauration d'arbres▲
Supposons maintenant le problème suivant : un certain programme ayant construit un arbre, on souhaite l'enregistrer dans un fichier en vue de son exploitation ultérieure par un autre programme. Deux difficultés font que ce travail n'est pas aussi simple que la sauvegarde d'un tableau :
- les nœuds de l'arbre n'occupent pas un espace contigu, ils sont en principe dispersés dans la mémoire et il faut parcourir l'arbre pour les retrouver ;
- même si on fait en sorte que les nœuds soient contigus, une difficulté demeure : la structure d'arbre est réalisée par des pointeurs, c'est-à-dire par des adresses dans la mémoire de l'ordinateur ; copiés dans un fichier, ces pointeurs perdent toute signification, car une recharge ultérieure de l'arbre en mémoire n'a aucune raison de « tomber » sur les mêmes adresses.
Il nous faudra donc inventer une sorte de syntaxe rudimentaire pour enregistrer l'arbre sans les pointeurs, de manière qu'il soit ensuite possible de le reconstituer par le programme devant l'exploiter. Nous supposerons que nous ne pouvons écrire sur le fichier de sauvegarde que des articles qui ont une même structure, à savoir celle du champ info des nœuds de l'arbre. Nous postulerons l'existence d'une valeur « impossible » du champ info, c'est-à-dire une valeur Ω qui ne peut être confondue avec aucune des valeurs réellement présentes dans l'arbre.
L'idée pour sauvegarder l'arbre ( I , ( A1 … An ) ), est la suivante :
- écrire la valeur I ;
- sauvegarder l'arbre A1 ;
- …
- sauvegarder l'arbre An ;
- écrire la valeur Ω.
Comme exemple, examinons les fonctions de sauvegarde et de restauration de l'arbre lexicographique défini à la section précédente. La partie info de chaque nœud étant un caractère, choisissons pour Ω la valeur ';' qui n'est pas une lettre possible. Voici ce qu'il faut ajouter au programme précédemment écrit :
#define OMEGA ';'
static FILE *fichier;Sauvegarde :
static void sauvegardeBis(POINTEUR p)
{
fputc(p->info, fichier);
for (p = p->fils; p != NULL; p = p->frere)
sauvegardeBis(p);
fputc(OMEGA, fichier);
}
void sauvegarde(POINTEUR arbre, char *nomfic)
{
if ((fichier = fopen(nomfic, "w")) == NULL)
erreurFatale(IMPOSSIBLE_CREER_FICHIER);
sauvegardeBis(arbre);
fclose(fichier);
}Restauration :
static char calu;
static POINTEUR restaurationBis(void)
{
POINTEUR p, f;
p = noeud(calu, NULL, NULL);
calu = fgetc(fichier);
if (calu != OMEGA)
{
f = p->fils = restaurationBis();
while (calu != OMEGA)
{
f->frere = restaurationBis();
f = f->frere;
}
}
calu = fgetc(fichier);
return p;
}
void restauration(POINTEUR *arbre, char *nomfic)
{
if ((fichier = fopen(nomfic, "r")) == NULL)
erreurFatale(IMPOSSIBLE_OUVRIR_FICHIER);
calu = fgetc(fichier);
*arbre = restaurationBis();
fclose(fichier);
}Essai de la sauvegarde :
sauvegarde(racine, "ArbreSauve");Essai de la restauration :
restauration(&racine, "ArbreSauve");Pour finir, imaginons qu'après avoir sauvegardé l'arbre donné en exemple, composé des mots main, mais, mal, mâle, mon, son, sono, sons et sont (voyez la figure 9), nous ayons bricolé une sorte de programme espion pour voir le contenu du fichier de sauvegarde, en affichant le caractère '\0' sous la forme @. Voici ce que nous y trouverons :
!main@;;s@;;;l@;e@;;;;on@;;;;son@;o@;;s@;;t@;;;;;;