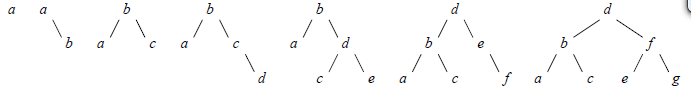3. Quelques arbres particuliers▲
3-1. Arbre maximier (tas), file de priorité▲
3-1-1. Arbres binaires complets et presque complets▲
De la même manière que les structures linéaires peuvent être implantées, avec différents avantages et inconvénients, soit par des structures chaînées, soit par des tableaux, une certaine catégorie d'arbres s'accommode très bien d'une représentation par tableaux.
Soit A un arbre binaire de hauteur k. Il est facile de prouver que :
- le nombre maximum de nœuds de niveau i est 2i-1 ;
- le nombre maximum de nœuds de A est 2k - 1.
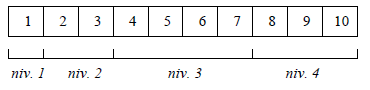
Un arbre binaire complet est un arbre binaire de hauteur k possédant 2k - 1 nœuds. Puisqu'il n'a pas de trous, un tel arbre peut être représenté par un tableau de 2k - 1 éléments, tout simplement en rangeant les valeurs des nœuds niveau par niveau(7) :
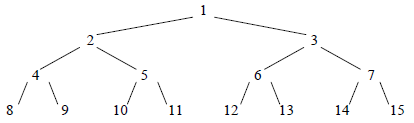

Soit N le nombre d'éléments du tableau (donc N = 2k - 1, k étant la hauteur de l'arbre). On a les propriétés suivantes :
- si kitxmlcodeinlinelatexdvpi \le Ent\left(\frac{N}{2}\right)finkitxmlcodeinlinelatexdvp, le fils gauche de Ti est T2i, le fils droit est T2i+1 ;
- si kitxmlcodeinlinelatexdvpi > Ent\left(\frac{N}{2}\right)finkitxmlcodeinlinelatexdvp, Ti est une feuille ;
- si j > 1, le père de Tj est kitxmlcodeinlinelatexdvpT_{Ent\left(\frac{N}{2}\right)}finkitxmlcodeinlinelatexdvp.
Un arbre binaire presque complet est un arbre binaire dont tous les niveaux sont pleins sauf le dernier, qui ne comporte que les p nœuds de gauche (un tel arbre n'est pas complet, mais au moins il n'a pas de trous). Dans une représentation par tableau définie comme pour les arbres binaires complets, il ne remplit donc que le début du tableau :
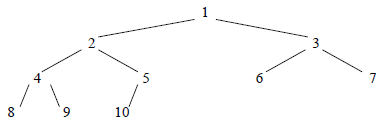
3-1-2. Arbres maximiers▲
Un arbre maximier, ou tas, est un arbre binaire presque complet, dont les nœuds ont un champ clé appartenant à un type ordonné, et tel que pour tout nœud p autre que la racine :
| clé(père(p)) ≥ clé(p) |
Par conséquent, la clé de la racine est le maximum des clés, d'où le nom de ces arbres. S'agissant d'arbres binaires presque complets, on les représente volontiers par des tableaux. Ainsi, un tableau T1… TN est la représentation d'un arbre maximier si, pour tout i = 1… N :
- 2i ≤ N ⇒ clé(T2i) ≤ clé(Ti) ;
- 2i + 1 ≤ N ⇒ clé(T2i+2) ≤ clé(Ti).
3-1-3. Files de priorité▲
Les files de priorité sont une des principales applications des arbres maximiers. Nous avons déjà étudié la notion de file d'attente, caractérisée par le fait que lorsqu'un élément est extrait de la file, c'est celui qui s'y trouve depuis le plus longtemps qui est extrait. Dans une file de priorité, les éléments de la file ont un champ, nommé priorité, dont les valeurs appartiennent à un type ordonné. Le comportement d'une file de priorité est défini par la propriété suivante : lors d'une extraction, c'est l'élément ayant la plus grande priorité qui est extrait.
Le rapport avec les arbres maximiers (prenant pour clé la priorité) est facile à voir : la racine d'un maximier est toujours l'élément ayant la plus grande priorité, donc le prochain qui devra être extrait. L'intérêt de cette manière d'implanter les files de priorité réside dans son efficacité :
- l'effort nécessaire pour extraire la racine d'un maximier (ou, plus exactement, pour refaire un maximier à partir d'un maximier décapité) est de l'ordre de log2N ;
- l'effort nécessaire pour introduire un élément dans un maximier, en le plaçant à l'endroit qui lui revient selon sa priorité, est de l'ordre de log2N.
Les algorithmes correspondants sont assez naturels : pour introduire un élément dans un arbre maximier, on le copie à la fin du tableau (dont le nombre d'éléments passe de N à N+1), ce qui en fait un fils, puis on le compare à son père. Si la relation qui doit exister entre un nœud et ses fils est satisfaite, l'insertion est terminée ; sinon, on permute le nouveau nœud et son père, ce qui fait du nouvel élément le fils d'un autre nœud, et on recommence.
Pour faire sortir la racine d'un maximier on fait à peu près le même travail, dans le sens contraire : on bouche le trou laissé par le nœud extrait avec le dernier élément du tableau (le nombre d'éléments de celui-ci passe de N à N-1), puis on vérifie si le nœud en question est bien placé par rapport à ses fils. Si c'est le cas on s'arrête, sinon on le permute avec le plus grand des deux fils, et on recommence.
Nous supposons avoir défini une macro PRIOR(x) donnant accès au champ priorité d'un élément (peut-être l'élément tout entier), et nous supposons que ce champ est d'un type supportant les opérateurs <, <=.
Ajout d'un élément à la file de priorité :
void entrer(OBJET x)
{
int i, j;
assert(N < TAILLE);
N++;
j = N;
while (j > 1)
{
i = j / 2;
if (PRIOR(t[i]) >= PRIOR(x))
break;
t[j] = t[i];
j = i;
}
t[j] = x;
}Extraction de l'élément dont c'est le tour :
OBJET sortir(void)
{
OBJET x, y;
int i, j;
assert(N > 0);
x = t[1];
y = t[N];
N--;
i = 1;
while ((j = 2 * i) <= N)
{
if (j + 1 <= N && PRIOR(t[j + 1]) > PRIOR(t[j]))
j++;
if (PRIOR(t[j]) < PRIOR(y))
break;
t[i] = t[j];
i = j;
}
t[i] = y;
return x;
}3-2. Arbres binaires équilibrés▲
3-2-1. Arbre binaire de recherche▲
Un arbre binaire de recherche (ABR) est un arbre binaire A dont les nœuds ont un champ clé, éventuellement le champ info tout entier, dont les valeurs appartiennent à un ensemble totalement ordonné, et qui vérifie, pour tout nœud r de A :
- pour tout nœud r' appartenant au sous-arbre gauche de r : r'.cle ≤ r.cle ;
- pour tout nœud r” appartenant au sous-arbre droit de r : r”.cle > r.cle.
L'arbre binaire de recherche correspondant à un ensemble de clés n'est pas unique : les deux ABR représentés dans la figure 5 correspondent aux mêmes clés. La structure précise de l'ABR est déterminée par l'algorithme d'insertion utilisé et par l'ordre d'arrivée des éléments.
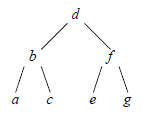 |
 |
| Déclarations : Sélectionnez |
La fonction rechInsertion recherche la clé x dans l'ABR pointé par rac. Si cette recherche est infructueuse, elle crée un maillon nouveau portant la clé x et l'insère dans l'arbre à la place voulue.
La version itérative d'une telle fonction est claire et efficace. Pour fixer les idées, nous en donnons ici une version récursive dont l'intérêt se manifestera ultérieurement.
void rechInsertion(CLE x, POINTEUR *rac)
{
int c;
if (*rac == NULL)
*rac = noeud(x, NULL, NULL);
else
if ((c = COMPAR(x, (*rac)->cle)) == 0)
EXPLOITER(*rac)
else
if (c < 0)
rechInsertion(x, &(*rac)->fg);
else
rechInsertion(x, &(*rac)->fd);
}3-2-2. Arbres équilibrés au sens des hauteurs (AVL)▲
L'intérêt des ABR réside dans le fait que, s'ils sont équilibrés, c'est-à-dire si chaque nœud a à peu près autant de descendants gauches que de descendants droits, alors
- la recherche d'un élément est dichotomique (c.-à-d. : à chaque étape la moitié des clés restant à examiner sont éliminées), et demande donc log2 n itérations ;
- l'insertion consécutive à une recherche a un coût nul.
Cela à la condition que l'arbre soit équilibré, car si on le laisse se déséquilibrer, les performances peuvent se dégrader significativement, jusqu'au cas tout à fait dégénéré de la figure 5, où l'arbre devient une liste chaînée, et la recherche devient séquentielle.
Nous allons examiner une méthode classique pour maintenir équilibré un arbre binaire de recherche. Auparavant, il faut préciser de quel équilibre on parle :
-
un arbre parfaitement équilibré est tel que pour chacun de ses nœuds r on a, à l'unité près :
cardinal ( sousArbreGauche( r ) ) = cardinal ( sousArbreDroit( r ) ) - un arbre équilibré au sens des hauteurs, ou AVL, est tel que pour chaque nœud r on a, à l'unité près :
| hauteur ( sousArbreGauche( r ) ) = hauteur ( sousArbreDroit( r ) ) |
L'effort à fournir pour garder un arbre parfaitement équilibré est très important. On se contente donc de l'équilibre des hauteurs, après avoir constaté que ce n'est pas un compromis trop mauvais : Adelson-Velskii et Landis (à l'origine de l'appellation AVL) ont montré que la hauteur d'un arbre binaire équilibré ne dépasse jamais de plus de 45 % la hauteur d'un arbre parfaitement équilibré ayant les mêmes clés(8).
Nous allons donc écrire une fonction de recherche et insertion qui maintiendra l'arbre équilibré. Pour cela, nous allons augmenter la fonction rechInsertion récursive déjà écrite.
Pour faire une insertion, la première version de la fonction rechInsertion fait une descente le long des branches de l'arbre, à la recherche de l'emplacement où le nouveau nœud se trouve ou doit être accroché. Nous lui ajouterons un travail à faire pendant la remontée vers la racine : examiner si, du fait de la création qui vient d'être faite, un nœud n'est pas devenu déséquilibré. Voici comment cela se présentera :
- après la création d'un nouveau nœud, durant la remontée vers la racine, on réagira sans tarder dès la rencontre d'un nœud déséquilibré ;
-
la rencontre d'un nœud déséquilibré déclenchera une réparation locale (bricolage de quelques pointeurs appartenant à quelques nœuds voisins) avec deux conséquences :
- dans le sous-arbre dont le nœud déséquilibré était la racine, il n'y aura plus de déséquilibre,
- ce sous-arbre, dont la hauteur avait augmenté (puisqu'il était devenu déséquilibré) sera revenu à la hauteur qu'il avait avant l'insertion, ce qui garantira l'équilibre de tous ses ancêtres.
L'équilibre d'un nœud est l'égalité des hauteurs de ses deux sous-arbres à l'unité près. Si un nœud devient déséquilibré (la hauteur d'un côté dépasse d'au moins deux unités la hauteur de l'autre côté) à la suite d'une insertion, c'est qu'avant cette insertion le nœud « penchait » déjà de ce côté. Savoir si un nœud penche d'un côté ou de l'autre est donc une information capitale. Pour en disposer, nous ajouterons un champ bal à chaque nœud, ainsi défini(9) :
kitxmlcodelatexdvpr.bal \left\{ \begin{matrix} -1, si hauteur(sousArbreGauche(r)) = hauteur(sousArbreDroit(r))+1 \\ 0, si hauteur(sousArbreGauche(r)) = hauteur(sousArbreDroit(r)) \\ +1, si hauteur(sousArbreGauche(r)) = hauteur(sousArbreDroit(r))-1 \end{matrix}\right.finkitxmlcodelatexdvpCommençons par déterminer les cas possibles. La situation est la suivante : après avoir descendu le long d'une branche de l'arbre, nous avons créé un nœud nouveau, nous l'avons accroché à une feuille, et nous avons entrepris de remonter vers la racine en revisitant chaque nœud par lequel nous étions passés lors de la descente, à la recherche du premier nœud que cette création a rendu déséquilibré.
Soit p ce nœud, supposons que l'ajout du nœud nouveau s'est faite dans son sous-arbre gauche ; le déséquilibre se traduit donc par hauteur(sousArbreGauche(p)) = hauteur(sousArbreDroit(p)) + 2, comme le montre la figure 6.
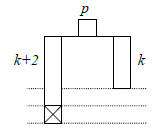
Bien entendu, il y a un autre cas possible, rigoureusement symétrique de celui-ci, nous n'en parlerons pas (mais nous le rencontrerons dans le programme final).
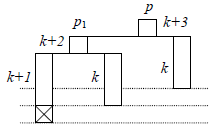
Examinons de plus près le sous-arbre gauche de p. Compte tenu du fait qu'on vient de faire la création d'un seul nœud, avant laquelle l'arbre était équilibré, il n'y a que deux configurations possibles:
 |
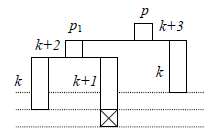 |
La réparation d'un nœud de type I s'appelle rotation simple :
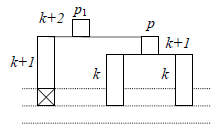
Pour la réparation d'un nœud de type II il faut examiner le fils droit de p1 (cf. figure 9). Notez que, des deux carrés barrés de cette figure, un seul existe (sinon l'arbre aurait été déséquilibré lors de l'insertion précédente), mais peu importe lequel est-ce.
On vérifie bien que, comme annoncé, la hauteur du sous-arbre déséquilibré après la correction du déséquilibre est la même que celle qu'avait le sous-arbre avant l'insertion.
Déclarations :
typedef char *CLE;
typedef struct noeud
{
CLE cle;
int bal;
struct noeud *fg, *fd;
} NOEUD, *POINTEUR;La nouvelle fonction rechInsertion possède un argument supplémentaire. Un appel comme :
rechInsertion(cle, arbre, &attention);recherche et au besoin crée un nœud portant la clé indiquée, dans l'arbre indiqué. Au retour, attention est vrai si cette opération a augmenté la hauteur de l'arbre (il y a donc lieu d'examiner l'état d'équilibre de sa racine).
void rechInsertion(CLE x, POINTEUR *p, int *attention)
{
int c;
POINTEUR p1, p2;
if (*p == NULL)
{
*p = noeud(x, 0, NULL, NULL);
*attention = 1;
}
else
if ((c = COMPAR(x, (*p)->cle)) == 0)
{
EXPLOITER(*p)
*attention = 0;
}
else
if (c < 0)
{
rechInsertion(x, &(*p)->fg, attention);
if (*attention)
if ((*p)->bal == 0)
(*p)->bal = -1;
else
if ((*p)->bal > 0)
{
(*p)->bal = 0;
*attention = 0;
}
else
{
p1 = (*p)->fg;
if (p1->bal < 0) /* type I */
{
(*p)->fg = p1->fd;
p1->fd = *p;
(*p)->bal = 0;
*p = p1;
}
else /* type II */
{
p2 = p1->fd;
p1->fd = p2->fg;
(*p)->fg = p2->fd;
p2->fg = p1;
p2->fd = *p;
if (p2->bal < 0)
p1->bal = 0, (*p)->bal = 1;
else
p1->bal = -1, (*p)->bal = 0;
*p = p2;
}
(*p)->bal = 0;
*attention = 0; /* le problème est éliminé */
}
}
else
{
// Cas symétrique du précédent : échangez fg et fd, < et >, -1 et +1.
}
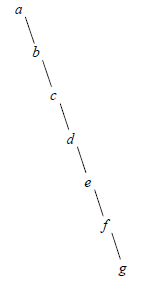
}Pour finir, voici deux tranches de la vie des AVL. La figure 10 montre une suite de rotations simples, provoquées par l'insertion successive, dans un arbre vide, de la suite de clés (a, b, c, d, e, f, g) (il s'agit justement la suite qui produit l'arbre dégénéré de la figure 5) :
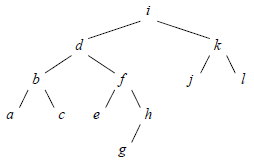
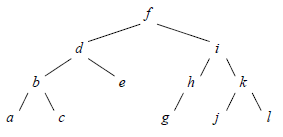
La figure 11 montre une double rotation provoquée par l'insertion de la clé g dans l'arbre de la figure 11 (a) :
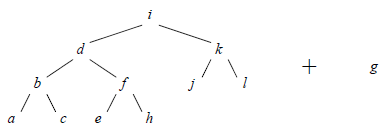 |
|
 |
 |
3-3. B-arbres▲
3-3-1. Position du problème▲
Comme dans les sections précédentes, nous nous intéressons à la recherche rapide d'un élément d'un ensemble de clés, chacune associée à une information, qui dépend de l'application particulière considérée.
Nous supposons maintenant que la taille totale de cet ensemble est si importante qu'il est hors de question de le conserver dans la mémoire primaire de l'ordinateur. Il se trouve donc sur une mémoire secondaire, en général un fichier sur disque magnétique. Ce fichier est constitué d'enregistrements, chacun pouvant être lu (chargé dans la mémoire) ou écrit (enregistré dans le fichier) indépendamment des autres, à partir de son rang dans le fichier.
Il y a ici une différence importante avec les problèmes étudiés précédemment : jusqu'à présent, pour faire vite on cherchait à optimiser l'ensemble des opérations effectuées. Or le transfert d'un enregistrement entre la mémoire secondaire et la mémoire primaire (ce que l'on appelle un « accès disque ») est tellement plus lent que les opérations internes, qu'il suffit de minimiser le nombre de ces transferts : tout gain de temps sur des opérations internes est négligeable devant le temps requis pour un accès disque.
Un premier cas simple est celui où le problème est posé par les informations associées, non par les clés. L'ensemble des clés est assez peu volumineux pour tenir dans la mémoire primaire. Il suffit alors de maintenir une table, appelée table d'index, dans laquelle chaque clé est associée au numéro de l'enregistrement la concernant. Cette table est gérée par une des méthodes expliquées dans les sections précédentes. L'accès à l'information correspondant à une clé donnée se fait en deux temps :
- ayant la clé, rechercher dans la table le rang de l'article correspondant ;
- ayant son rang, transférer l'article en question depuis ou vers le fichier.
Ici, nous allons nous intéresser plutôt au cas où l'ensemble des clés est lui-même beaucoup trop volumineux, pour pouvoir être conservé dans la mémoire principale.
3-3-2. B-arbres▲
Nous avons remarqué l'intérêt des arbres binaires équilibrés. Pour trouver une clé dans un arbre binaire d'un million de nœuds, il faut seulement une vingtaine d'accès aux nœuds de l'arbre, puisque 220 ~ 106. Mais si chaque accès à un nœud implique le chargement d'un enregistrement d'un fichier sur disque magnétique, cela fait encore beaucoup trop.
Les B-arbres sont une manière efficace, élégante et assez simple de conserver les avantages des arbres équilibrés tout en les adaptant aux caractéristiques particulières des fichiers. Bien sûr, l'idée de départ est de gonfler les nœuds et de leur faire porter plus d'une clé. Par exemple, avec des nœuds d'une capacité maximale de 100 clés, un B-arbre contenant un million de clés aura entre 10.000 et 20.000 nœuds et pour retrouver une clé il faudra 3,2 accès à un nœud, en moyenne, et 3,5 dans le pire des cas.
La structure d'un B-arbre est la généralisation de celle d'un ABR : à la place d'une clé et deux pointeurs, chaque nœud porte k clés c0, c1… ck-1 et k+1 pointeurs p-1, p0… pk-1. Les clés sont triées par ordre croissant. Le pointeur pi renvoie à un nœud qui est la racine d'un sous-arbre Ai contenant les clés c qui vérifient ci < c < ci+1.
Cas particuliers, p-1 pointe le sous-arbre des clés vérifiant c < c0 et pk-1 pointe le sous-arbre des clés vérifiant ck-1 < c (en réalité, ces clés extrêmes ont elles aussi des bornes à droite et à gauche, héritées du père du nœud en question).
Les nœuds des B-arbres sont appelés pages ; chacune correspond à un enregistrement du fichier sous-jacent. Lorsque la capacité d'une page (la valeur maximum de k) est 2N, on dit que l'on a affaire à un B-arbre de degré N. L'algorithme de manipulation que nous allons présenter garantit que :
- chaque page, sauf la racine, porte au moins N clés ;
- une page qui porte k clés et qui n'est pas une feuille possède k+1 filles ;
- toutes les feuilles sont au même niveau ; du point de vue de la hauteur, l'arbre est donc équilibré.
INSERTION D'UNE CLÉ
La procédure d'insertion est responsable du maintien des propriétés ci-dessus. Comme pour les arbres binaires, une insertion se produit à la suite d'une recherche infructueuse qui a consisté à descendre le long d'une branche de l'arbre, jusqu'à une feuille qui a montré que la clé cherchée n'existait pas. Deux cas sont alors possibles.
- La feuille en question n'est pas saturée (k < 2N) : il s'agit d'une insertion ordinaire dans une table triée.
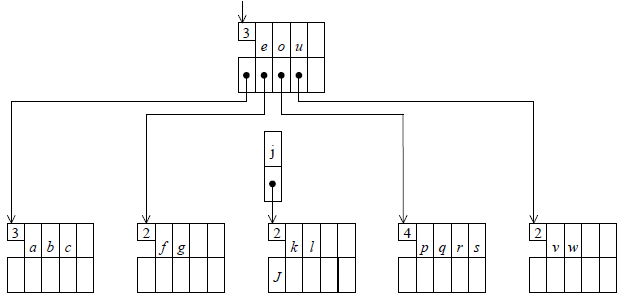
- La feuille est pleine (k = 2N). On a représenté par J l'éventuel pointeur associé à la clé j :
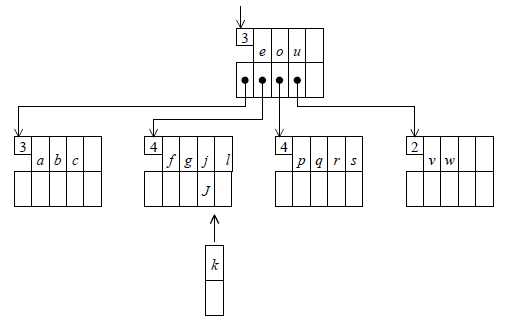
On effectue la scission de la page, qui produit deux pages à moitié pleines et un élément à insérer dans la page mère :
Dans le partage d'une page à 2N clés en deux pages à N clés, chaque clé voyage avec son information associée. Un petit trafic de pointeurs a lieu, mais on vérifie aisément que c'est celui qu'il faut pour que les propriétés du B-arbre soient vérifiées : la clé qui « s'en va » cède sa descendance éventuelle à la nouvelle page, à titre de pointeur p-1, et elle prend pour descendance la nouvelle page. Bien entendu, si la page mère est pleine elle aussi, alors elle se scindera à son tour en deux pages à demi pleines et fera remonter un élément vers sa propre page mère, etc.
Cas particulier : si la page qui est pleine n'a pas de mère, c'est-à-dire s'il s'agit d'une insertion dans la racine (saturée), alors cette dernière se divise en deux et il y a création d'une nouvelle racine avec une unique clé et deux descendants.
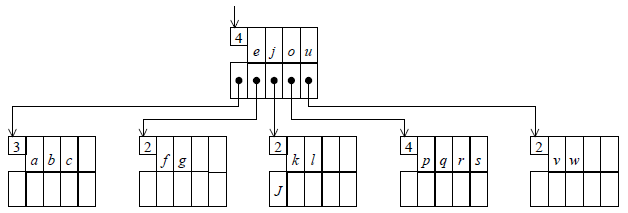
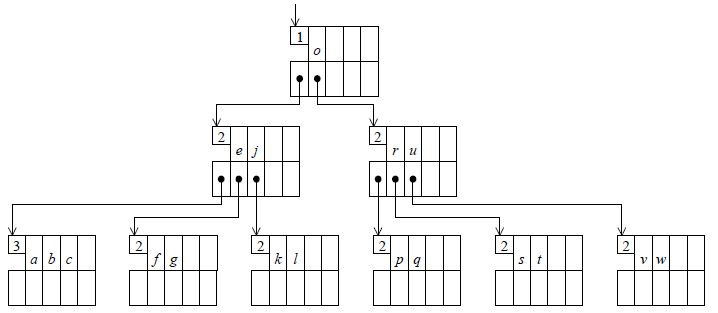
Ainsi, par exemple, la figure 13 montre le résultat d'une scission de la racine, provoquée par l'insertion de la clé t dans le B-arbre de la figure 12.
Les B-arbres ont une curieuse façon de croître : ce sont les feuilles qui font pousser l'arbre du côté de la racine !
3-3-3. Implantation des B-arbres▲
Ce que nous avons appelé pointeurs dans les explications précédentes sont en fait des renvois à des enregistrements d'un fichier permettant l'accès relatif, c'est-à-dire des nombres exprimant les rangs de ces enregistrements. L'opération fondamentale d'un pointeur ordinaire, l'accès à la variable pointée, se traduira ici par un travail beaucoup plus important, le chargement en mémoire de l'enregistrement en question. Pour ne pas entrer dans les détails de l'accès aux fichiers, nous supposerons disposer des trois primitives suivantes :
void charger(PAGE *adrPage, long rang);cette fonction copie dans la page (en mémoire) pointée par adrPage la composante du fichier ayant le rang indiqué ;
void ranger(PAGE *adrPage, long rang);cette fonction copie la page (en mémoire) pointée par adrPage sur la composante du fichier ayant le rang indiqué.
long allouerPage(void);Cette fonction détermine et renvoie le rang d'un emplacement libre dans le fichier. Nous supposerons que cette opération réussit toujours.
Nous postulerons enfin qu'une composante d'un fichier ne peut pas avoir le rang -1. Cette valeur tiendra donc ici le rôle du pointeur impossible (NULL).
Déclarations globales :
typedef … CLE; /* dépend de l'application */
#define N … /* le degré du B-arbre */
typedef struct item
{
CLE cle;
long p;
... /* autres informations associées aux clés */
} ITEM;
typedef struct page
{
int k;
long p_1; /* le pointeur p[-1] */
ITEM t[2 * N];
} PAGE;
#define NIL (-1)Nous supposons posséder par ailleurs la fonction :
int existe(CLE cle, PAGE *page, int *pos)qui cherche la cle indiquée dans la page indiquée. La fonction rend 1 si la clé s'y trouve (*pos renvoie alors à son indice), 0 si elle ne s'y trouve pas (*pos renvoie alors à l'indice où il faudrait l'insérer pour respecter l'ordre) ; il s'agit de la recherche dichotomique dans une table triée.
RECHERCHE
La fonction suivante rend 1 ou 0 pour traduire le succès ou l'échec de la recherche de la cle indiquée dans l'arbre dont la racine est la page ayant l'adresse indiquée. Cette fonction peut s'écrire aussi simplement de manière itérative ; nous en donnons une version récursive en vue de la fonction de recherche-insertion qui va suivre et qui, elle, gagnera à être récursive :
int recherche(CLE cle, long adresse)
{
PAGE A;
int i;
if (adresse == NIL)
return 0;
else
{
charger(&A, adresse);
if (existe(cle, &A, &i))
{
EXPLOITER(A.t[i])
return 1;
}
else
return recherche(cle, i == 0 ? A.p_1 : A.t[i - 1].p);
}
}Remarque sur la variable A. Déclarée comme ci-dessus, c'est-à-dire locale à la fonction de recherche, il existe à un moment donné autant d'exemplaires de la variable A que d'activations de la fonction. Il ne faut pas que cela dépasse la capacité de la mémoire principale.
Nous obtenons ainsi une limitation pour la taille N des pages, et un mode d'estimation de la valeur adaptée aux besoins et possibilités d'une application particulière. Soit T la taille globale de l'ensemble des clés, N le degré du B-arbre.
Dans le cas le plus défavorable (les pages ne sont remplies qu'à 50 %) la hauteur de l'arbre est
| kitxmlcodeinlinelatexdvppr_N = \frac{logT}{logN}-1finkitxmlcodeinlinelatexdvp |
Dans la recherche-insertion d'un élément on peut avoir jusqu'à prN activations de la fonction, chacune ayant alloué sa propre page; une page auxiliaire est parfois nécessaire dans le cas de l'insertion. L'encombrement total sera donc de :
| kitxmlcodeinlinelatexdvpe_N \cong 2N*sizeof(ITEM)*\frac{logT}{logN}finkitxmlcodeinlinelatexdvp |
Nous devrons donc prendre la plus grande valeur de N telle que eN soit inférieur ou égal à l'espace disponible. Nous aurons ainsi la meilleure valeur de prN.
RECHERCHE-INSERTION
Cette opération est assurée par deux fonctions complémentaires :
void rechInser(CLE cle, long adresse, int *att, ITEM *v);cette fonction recherche et au besoin insère la cle donnée dans l'arbre dont la racine est la page ayant l'adresse indiquée. Au retour, *att est vrai lorsque cette insertion a projeté « vers le haut » un item, qu'il fait insérer dans la page mère ; *v est alors cet item ;
void inserItem(PAGE *p, ITEM u, int pos, int *att, ITEM *v);cette fonction insère l'item u, à la position indiquée par pos, dans la page (en mémoire) pointée par p. Au retour, *att est vrai si cette opération a projeté vers le haut un item, qu'il faut insérer dans la page mère ; *v est alors cet item.
Voici les textes de ces fonctions :
void inserItem(PAGE *, ITEM, int, int *, ITEM *);
void rechInser(CLE cle, long adresse, int *att, ITEM *v)
{
PAGE A;
int i;
if (adresse != NIL)
{
charger(&A, adresse);
if (existe(cle, &A, &i))
{
EXPLOITER(A.t[i])
*att = 0;
}
else
{
rechInser(cle, i == 0 ? A.p_1 : A.t[i - 1].p, att, v);
if (*att)
{
inserItem(&A, *v, i, att, v);
ranger(&A, adresse);
}
}
}
else
{ /* un item nouveau est traité */
v->cle = COPIE(cle); /* comme un item produit par */
v->p = NIL; /* la scission d'une page */
*att = 1; /* (fictive) */
}
}void inserItem(PAGE *p, ITEM u, int pos, int *att, ITEM *v)
{
int i;
if (p->k < 2 * N) /* insertion sans problème */
{
for (i = p->k; i > pos; i--)
p->t[i] = p->t[i - 1];
p->t[pos] = u;
p->k++;
*att = 0;
}
else /* scission de page (aïe...!) */
{
PAGE B;
long adresseB = allouerPage();
/* le fatras qui suit fait la */
if (pos <= N) /* distribution sur deux pages */
{ /* des clés en jeu */
if (pos == N)
*v = u;
else
{
*v = p->t[N - 1];
for (i = N - 1; i > pos; i--)
p->t[i] = p->t[i - 1];
p->t[pos] = u;
}
for (i = 0; i < N; i++)
B.t[i] = p->t[i + N];
}
else
{
*v = p->t[N];
for (i = N + 1; i < pos; i++)
B.t[i - (N + 1)] = p->t[i];
B.t[pos - (N + 1)] = u;
for (i = pos; i < 2 * N; i++)
B.t[i - N] = p->t[i];
}
p->k = B.k = N;
B.p_1 = v->p;
v->p = adresseB;
/* on sauve la page B (A le sera */
ranger(&B, adresseB); /* par la fonction appelante) */
*att = 1;
}
}L'appel initial de rechInser se fait de la manière suivante (appel, éventuellement suivi de la scission de la racine) :
long adRacine; /* rang de la page qui est */
/* la racine du B-arbre) */
void inserer(CLE cle)
{
PAGE a;
ITEM u;
int scission;
long r;
rechInser(cle, adRacine, &scission, &u);
if (scission)
{
r = allouerPage();
a.p_1 = adRacine;
a.k = 1;
a.t[0] = u;
ranger(&a, r);
adRacine = r;
}
}