4. Recherche rapide▲
4-1. Recherche rapide▲
Nous posons le problème suivant : organiser une collection d'informations, chacune associée à une clé qui l'identifie de manière unique, de façon à pouvoir retrouver (sous-entendu : le plus vite possible) une clé et l'information qui lui est associée. Nous supposerons que les clés sont des chaînes de caractères.
Dans les applications, ce problème apparaît sous deux variantes principales :
- les dispositifs de type fichier indexé, où la clé est l'accès biunivoque à une information beaucoup plus volumineuse, qui se trouve généralement dans une mémoire secondaire ;
- les dispositifs de type dictionnaire, où l'ensemble de la structure se trouve en mémoire centrale, car l'information associée à chaque clé est peu volumineuse. Exemple : le dictionnaire que gère un compilateur, contenant les identificateurs du programme en cours de compilation.
Le mécanisme réalisé doit permettre les opérations de recherche, insertion et suppression d'un couple (clé, info). On cherche à optimiser la recherche sans pénaliser l'insertion. La suppression, parfois sans objet, est rarement optimisée.
4-1-1. Méthodes connues▲
RECHERCHE SEQUENTIELLE
Recherche. La fonction suivante renvoie 1 ou 0 selon que la valeur x figure ou non dans le tableau t de n éléments. En cas de succès, la fonction range dans la variable pointée par rang la valeur de l'indice de l'élément dans le tableau :
int existe(CLE x, CLE t[], int n, int *rang)
{
int i;
for (i = 0; i < n; i++)
if (COMPAR(t[i], x) == 0)
{
*rang = i;
return 1;
}
return 0;
}Recherche avec insertion :
if (existe(x, t, n, &position))
EXPLOITER(table[position])
else
t[n++] = COPIE(x);N.B. Le type CLE et la fonction COMPAR sont jumelés. La fonction COPIER dépend en plus de la nature du tableau t.
Exemple (très critiquable, car pour bien faire il faudrait tester la réussite de l'appel de malloc) :
typedef char *CLE;
#define COMPAR(a, b) strcmp(a, b)
#define COPIE(x) strcpy(malloc(strlen(x) + 1), x)Coût moyen :
- d'une recherche : n/2 ;
- d'une insertion : 1 (autant dire : rien).
RECHERCHE DICHOTOMIQUE
Principe : le tableau est trié ; à chaque étape, on le découpe en deux moitiés et, en comparant la valeur cherchée avec la valeur de l'élément médian, on élimine celle des deux moitiés qui ne peut pas contenir la valeur cherchée.
La fonction suivante renvoie 1 ou 0 selon que la valeur x figure ou non dans le tableau trié t de n éléments. La variable pointée par rang est affectée par le rang de l'élément cherché, si ce dernier existe dans le tableau, sinon elle est affectée par le rang où il faudra ranger x si on veut l'insérer en conservant le tableau trié :
int existe(CLE x, CLE t[], int n, int *rang)
{
int i, j, k;
i = 0;
j = n - 1; /* assertion: que x soit présent ou absent */
while (i <= j) /* son rang r vérifie: i <= r <= j + 1 */
{
k = (i + j) / 2;
if (COMPAR(x, t[k]) <= 0)
j = k - 1;
else
i = k + 1;
}
/* ici, en outre: i = j + 1 */
*rang = i;
return i < n && COMPAR(t[i], x) == 0;
}Recherche avec insertion :
if (existe(x, t, n, &position))
EXPLOITER(table[position])
else
{
for (i = n; i > position; i--)
t[i] = t[i - 1];
t[position] = COPIE(x);
n++;
}Coût moyen :
- d'une recherche : log2n ;
- d'une insertion : n/2.
En conclusion, la recherche dichotomique est une excellente méthode de recherche, mais les insertions coûtent cher.
ARBRE BINAIRE DE RECHERCHE, ARBRE AVL
Les arbres binaires de recherche offrent l'efficacité de la recherche dichotomique (du moins si l'on prend soin de les garder équilibrés, comme les AVL) sans le coût de l'insertion dans un tableau ordonné. Les AVL font l'objet du § 3.2Arbres binaires équilibrés.
ARBRE LEXICOGRAPHIQUE
Citons, pour mémoire, l'arbre lexicographique développé au § 2.5.1Arbre lexicographique (codage en parties communes). Son principal avantage réside dans le fait qu'une recherche prend un temps qui ne dépend que de la longueur de la clé, non du nombre de clés.
Exemple (théorique) : avec des clés longues de 8 caractères, si on suppose que pour chaque caractère il y a six choix en moyenne, on pourra gérer 68 (~ 1,7 millions) clés, alors qu'une recherche ou une insertion moyenne ne nécessitera que 3 × 8 = 24 opérations.
L'inconvénient majeur de l'arbre lexicographique est le surencombrement créé par l'information de service (les pointeurs fils et frere). Ainsi, la partie « solitaire » d'un mot, c'est-à-dire les caractères qui ne sont pas partagés avec d'autres mots, occupe au moins neuf octets par caractère. Selon la nature de l'ensemble de clés manipulées, cette dépense peut se révéler prohibitive.
4-1-2. Adressage dispersé (hash-code)▲
Les méthodes de la famille « hash-code », ou adressage dispersé, sont les plus employées, car elles dépassent en efficacité toutes les précédentes.
L'idée de base est la suivante : pour trouver une clé donnée dans un tableau on ne fait pas une recherche, mais un calcul à partir de la clé, beaucoup plus rapide.
Si C est l'ensemble des clés possibles, et si T0 … TN-1 est le tableau contenant les clés effectives, on se donne donc une fonction, à évaluation peu onéreuse :
| h : C → { 0, 1… N-1 } |
et on espère (c'est une utopie) que :
| pour toute clé effective c, l'emplacement de c est Th(c) |
Bien entendu, l'idéal serait d'avoir une fonction h bijective (c.-à-d. h atteint tous les indices du tableau et à deux clés différentes h associe des indices différents). Cela est impossible, parce que l'ensemble des clés effectives est un sous-ensemble peu connu, voire tout à fait inconnu, de l'ensemble des clés possibles, qui est souvent gigantesque. On se contente donc de fonctions qu'on pourrait appeler « bijectives avec des ratés », et on met en place un mécanisme pour prendre en charge les « ratés », que l'on appelle des collisions. Il y a collision lorsque la fonction h donne la même valeur pour deux clés distinctes c1 et c2:
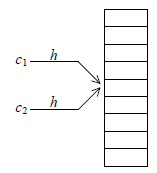
Le premier travail, dans la mise en place d'un dispositif d'adressage dispersé, est donc le choix d'une fonction d'adressage h : C → { 0, 1… N-1 }. À cette fonction on demande essentiellement de posséder deux qualités :
- être facile à calculer, car nous voulons une méthode rapide ;
- être uniforme : la probabilité pour que h(c) soit égale à v doit être la même pour toutes les valeurs 0 ≤ v ≤ N-1, c'est-à-dire il ne faut pas qu'à certains endroits de la table se produisent de nombreuses collisions, tandis qu'à d'autres endroits des cases restent libres.
Trouver une bonne fonction d'adressage est un problème difficile, que l'on résout souvent empiriquement : on choisit une fonction et on « espionne » le fonctionnement global du système durant quelque temps. On améliore la fonction, on espionne de nouveau et ainsi de suite. En outre, on fait confiance aux recettes transmises par les anciens, comme :
- c'est mieux si N, la taille de la table, est un nombre premier ; en aucun cas N ne doit être une puissance de 2 ;
- les fonctions de la forme h(c) ≡ h0(c) mod N (c'est le cas de la plupart des fonctions) sont d'autant meilleures que h0 fournit des valeurs très grandes.
Exemples de fonctions d'adressage : en supposant qu'une clé est une chaîne de caractères, notée c0c1…cn-1 :
| h1(c) = (c0 - 'A') mod N |
Attention, h1 est une très mauvaise fonction, car elle n'est pas uniforme. En voici une meilleure : elle consiste à prendre un mot comme l'écriture d'un nombre en base 26 (puisqu'il y a 26 lettres)
| h2(c) = (c0 + c1 × 26 + c2 × 262 + … + ck × 26k ) mod N |
Remarque : les fonctions du style de h2 sont utilisées très fréquemment. Elles justifient le conseil « la taille de la table doit être un nombre premier ». Imaginez que N soit égal à 26 : h2 devient analogue à h1 ! Si N n'est pas 26 mais possède des diviseurs communs avec 26, certains termes du polynôme ci-dessus seront systématiquement nuls et la répartition des valeurs fournies par la fonction ne sera pas être uniforme. Prendre N premier est un moyen d'écarter ces défauts.
CHAÎNAGE EXTERNE
Intéressons-nous maintenant à la résolution des collisions. Il existe principalement deux manières de s'y prendre : le chaînage externe et le chaînage interne (ou chaînage ouvert).
Dans le chaînage externe la fonction h d'adressage ne sert pas à adresser une table de clés, mais une table de listes chaînées, chacune constituée des clés pour lesquelles h fournit la même valeur.
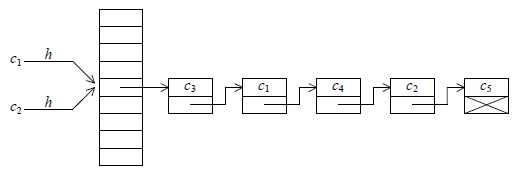
La recherche ou l'insertion d'un élément se font en deux temps :
- utilisation de la fonction d'adressage pour obtenir la tête de la liste susceptible de contenir la clé recherchée ;
- parcours séquentiel de cette liste en recherchant la clé en question.
Les programmes correspondants sont laissés au lecteur à titre d'exercice.
Cette méthode convient particulièrement aux ensembles très dynamiques, avec de nombreuses insertions et suppressions, notamment lorsqu'il est difficile ou impossible d'estimer à l'avance le nombre de clés qu'il faudra mémoriser. Dans cette optique, le chaînage externe, que nous avons présenté en parlant de collisions (le mot collision suggère l'idée d'un événement exceptionnel, un « raté » de la fonction d'adressage) apparaît plutôt comme une méthode de partitionnement des clés : étant donné une clé, un moyen rapide, la fonction h détermine le compartiment susceptible de contenir cette clé, et dans lequel on fait une recherche séquentielle. Ici, la collision de deux clés signifie simplement qu'elles habitent dans le même compartiment et n'a rien d'exceptionnel.
CHAÎNAGE INTERNE
Le chaînage interne, au contraire, suppose qu'on a d'avance une bonne connaissance du nombre des clés qui seront à gérer et que l'on a décidé de les ranger dans un tableau possédant une taille suffisante pour les loger toutes. On ne veut donc pas payer le surencombrement dû aux pointeurs des listes chaînées. Ici, l'adressage dispersé est vu comme un substitut de l'indexation, et les collisions comme des accidents regrettables qu'une meilleure fonction d'adressage et une meilleure connaissance de l'ensemble des clés auraient pu éviter.
Le principe du chaînage interne est le suivant :
- les cases du tableau adressé par la fonction d'adressage sont occupées par les clés elles-mêmes ; il existe une valeur de clé conventionnelle pour indiquer qu'une case est libre (nous la noterons LIBRE) ;
-
recherche : lorsque la fonction h, appliquée à une clé c1, donne l'indice h(c1) d'une case occupée par une autre clé, on parcourt le tableau à partir de h(c1). Cette recherche s'arrête dès la rencontre :
- d'une case contenant la clé c1, qui signifie le succès de la recherche;
- d'une case libre, qui signifie l'échec de la recherche ;
-
insertion : comme la recherche, en s'arrêtant dès la rencontre :
- d'une case contenant c1 (l'insertion est refusée, puisqu'on ne veut pas de doublon),
- d'une case libre: la clé c1 est insérée à cet endroit
Bien entendu, le tableau est parcouru circulairement : la première case suit logiquement la dernière. De plus, on fait en sorte qu'il y ait constamment au moins une case libre dans le tableau.
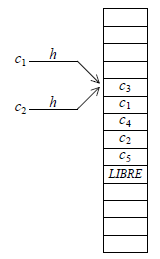
Recherche :
typedef char *CLE;
#define N 101
CLE t[N];
#define LIBRE NULL
#define SUIVANT(i) (((i) + 1) % N)
static int hash(CLE s)
{
int r = 0;
while (*s != 0)
r = (26 * r + (*s++ - 'A')) % N;
return r;
}
int recherche(CLE cle)
{
int h;
h = hash(cle);
while (t[h] != LIBRE && COMPAR(t[h], cle) != 0)
h = SUIVANT(h);
return t[h] != LIBRE ? h : -1;
}L'insertion n'est pas très différente de la recherche :
void insertion(CLE cle)
{
int h;
if (nbre_elements >= N - 1)
erreurFatale(TABLE_PLEINE);
h = hash(cle);
while (t[h] != LIBRE && COMPAR(t[h], cle) != 0)
h = SUIVANT(h);
if (t[h] != LIBRE)
erreurFatale(CLE_DEJA_INSEREE);
t[h] = COPIE(cle);
nbre_elements++;
}La suppression requiert quelques précautions. Pour nous en convaincre, imaginons que la clé d'indice h (voyez la figure 4) doive être supprimée, et considérons la clé d'indice p qui se trouve après h alors que son hash-code hp correspond à une case qui se trouve devant h. Si, pour supprimer la clé d'indice h, nous nous contentions de la remplacer par la valeur LIBRE, nous mettrions la table dans un état incohérent dans lequel la clé d'indice p serait devenue inaccessible : sa recherche commencerait à la case d'indice hp et serait arrêtée par la case libre d'indice h.
Pour éviter cette incohérence, le programme de suppression passe en revue toutes les clés qui sont ainsi susceptibles de devenir inaccessibles. Ce sont les clés (cf. figure 3) :
- qui se trouvent entre la case d'indice h et la première case vide après celle-là ;
- dont le hash-code renvoie à une case qui se trouve entre la dernière case vide devant la case h et la case h.
Nous utilisons la pseudo-fonction COMPRIS_ENTRE(a, b, c) pour caractériser le fait que l'indice a est compris entre les indices b et c en tenant compte du fait que le tableau est circulaire :
#define SUIVANT(i) (((i) + 1) % N)
#define PRECEDENT(i) (((i) + (N - 1)) % N)
#define COMPRIS_ENTRE(a, b, c) \
((b < c && (b <= a && a <= c)) || \
(c < b && (a <= c || b <= a)))Nous avons le programme :
void suppression(CLE cle)
{
int h, b, p, hp;
h = hash(cle);
while (t[h] != LIBRE && COMPAR(t[h], cle) != 0)
h = SUIVANT(h);
if (t[h] == LIBRE)
erreurFatale(CLE_ABSENTE);
b = h;
while (t[b] != LIBRE)
b = PRECEDENT(b);
for (;;)
{
t[h] = LIBRE;
for (p = SUIVANT(h);; p = SUIVANT(p))
{
if (t[p] == LIBRE)
return;
hp = hash(t[p]);
if (COMPRIS_ENTRE(hp, b, h))
{
t[h] = t[p];
h = p;
break;
}
}
}
}HACHAGE
Un risque majeur, dans les dispositifs de chaînage interne, est le danger d'entrelacement des listes de collisions. Avec le programme précédent si, par un défaut de la fonction d'adressage, les clés ont tendance à se regrouper en une région du tableau, notre manière de résoudre les collisions augmentera encore cet effet d'entassement. Le système deviendra alors inefficace, car les accès à la table se traduiront par des recherches de plus en plus séquentielles.
Une manière de résoudre ce problème consiste à améliorer la méthode de « sondage », c'est-à-dire la manière de chercher la case voulue à partir de la case indiquée par la fonction h.
Ce que nous avons programmé plus haut est le sondage séquentiel. Pour en montrer l'inconvénient, imaginons que deux clés c1 et c2 aient des hash-codes consécutifs : h1 = h(c1), h2 = h(c2) et h2 = h1+1. Les cases qui seront sondées sont
- dans la recherche de c1 : h1, h1+1, h1+2, h1+3…
- dans la recherche de c2 : h2 = h1+1, h1+2, h1+3…
Les listes de collision correspondant à h1 et à h2 se sont entremêlées : des clés qui n'auraient dû intervenir que dans la recherche de c1 ou que dans celle de c2 sont examinées lors de la recherche de c1 et lors de celle de c2.
Une meilleure méthode est le sondage quadratique, consistant à examiner, pour la recherche ou l'insertion d'une clé c, les cases d'indices :
| h0 = h(c), h1 = (h0 + 12) mod N, h2 = (h0 + 22) mod N… hi = (h0 + i2) mod N |
Une méthode encore meilleure est l'adressage double, ou hachage, consistant à examiner :
| h0 = h(c), h1 = (h0 + uc) mod N, h2 = (h0 + 2 x uc) mod N… hi = (h0 + i x uc) mod N |
où uc est une constante donnée par une deuxième fonction d'adressage :
| uc = h'(c) |
La fonction de hachage h' doit respecter quelques principes simples :
- elle doit éviter la valeur 0,
- N (la taille du tableau) et uc doivent être premiers entre eux (sinon les hi ne décrivent pas tout le tableau),
- plus généralement, h' ne doit pas être « parente »(10) avec h, pour éviter des consanguinités susceptibles de créer des accumulations assez vicieuses.
4-2. Recherche de motifs dans des chaînes▲
Le problème que nous étudions ici n'est pas de même nature que le précédent. Il s'agit toujours de rechercher rapidement une clé, mais maintenant nous ne la cherchons plus dans un ensemble de clés habilement structuré en vue d'optimiser les recherches, mais au contraire dans une collection d'informations élémentaires « en vrac ». Cas typique : la recherche d'un mot dans un texte.
On se donne un ensemble E, deux suites d'éléments de E, notées M = (m0 m1 … mlm-1), le motif et C = (c0 c1 … clc-1), la chaîne, vérifiant lc ≥ lm, et on recherche la première occurrence de M dans C, c'est-à-dire le plus petit indice i vérifiant :
| i + lm ≤ lc |
et :
| mj = ci+j pour j = 0, 1… lm-1. |
Ce problème se présente souvent, et sous des formes qui font aisément comprendre l'importance d'avoir un algorithme efficace. Des exemples :
- recherche d'information : E est l'ensemble des caractères, et on cherche un mot ou une expression dans le texte d'une encyclopédie, dans tous les fichiers d'un ordinateur, dans toutes les pages du Web, etc. ;
- recherches en génétique : E = { ‘A', ‘T', ‘G', ‘C' } et on recherche une configuration donnée dans une chaîne d'ADN décrite par une suite de plusieurs millions d'occurrences de ces lettres ;
- traitement de formes (images, sons…) : E = { 0, 1 } et on recherche une configuration binaire donnée dans une suite de plusieurs milliards de 0 et 1.
Pour fixer les idées, nous supposerons ici que E est l'ensemble des caractères du langage de programmation utilisé.
4-2-1. Algorithme naïf▲
Un algorithme de recherche découle immédiatement de la définition donnée :
int recherche(char m[], int lm, char c[], int lc)
{
int i, j, imax = lc - lm;
for (i = 0; i <= imax; i++)
{
for (j = 0; j < lm; j++)
if (m[j] != c[i + j])
break;
if (j >= lm)
return i; /* succès */
}
return -1; /* échec */
}La complexité en moyenne de cet algorithme est Θ(lm × lc).
Plusieurs méthodes permettent d'avoir Θ(lm + lc). Elles obtiennent un tel gain en effectuant un travail préalable, une étude du motif, avant de commencer le parcours de la chaîne.
4-2-2. Automate d'états finis▲
La méthode consiste à construire un automate d'états finis qui reconnaît le motif donné. Le nombre d'opérations est k × lm + lc. Si lc est important devant lm, cette méthode est certainement la meilleure.
4-2-3. Algorithme de Knuth, Morris et Pratt▲
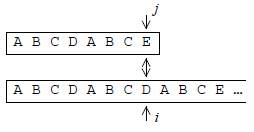
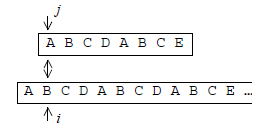
On peut présenter cette méthode en critiquant la méthode naïve. Cette dernière consiste à « aligner » les caractères du motif avec ceux de la chaîne à partir d'une position i, puis à avancer de concert, sur le motif et sur la chaîne, tant que les caractères correspondants coïncident :
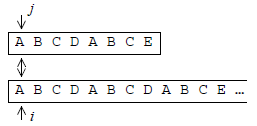 |
 |
 |
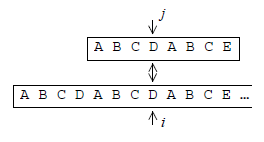 |
La méthode de Knuth, Morris et Pratt part de la remarque suivante : si la discordance se produit sur le caractère ci+p c'est que les caractères (ci ci+1 … ci+p-1) de la chaîne coïncident avec les caractères (m0 m1 … mp-1) du motif. Il devrait donc être possible, par une étude préalable du motif, de « précalculer » une fois pour toutes les conduites efficaces à adopter lorsqu'un appariement échoue.
En fait, dans l'algorithme de KMP on arrive à ne jamais reculer l'indice i sur la chaîne, comme le montre la figure 8, en calculant au préalable dans une table suivant, pour chaque caractère du motif, la valeur à donner à l'indice j lorsqu'une discordance se produit sur ce caractère.
Pour le motif « ABCDABCE », le tableau suivant est :
| A | B | C | D | A | B | C | E |
| -1 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |
Dans l'exemple de la figure 6, la discordance s'est produite pour j = 7, et suivant[7] = 3 ; d'où l'état de la figure 8.
La fonction de recherche peut s'écrire ainsi :
int recherche_KMP(char m[], int lm, char c[], int lc, int suivant[])
{
int i, j;
for (i = j = 0; j < lm && i < lc; i++, j++)
while (j >= 0 && c[i] != m[j])
j = suivant[j];
if (j == lm)
return i - lm; /* succès */
else
return -1; /* échec */
}La fonction qui calcule le tableau suivant à partir du motif ressemble à une recherche du motif dans lui-même :
void initSuivant(char *m, int lm, int suivant[])
{
int i, j;
suivant[0] = -1;
j = -1;
i = 0;
while (i < lm - 1)
{
while (j >= 0 && m[i] != m[j])
j = suivant[j];
suivant[++i] = ++j;
}
}