II. Analyse lexicale▲
L'analyse lexicale est la première phase de la compilation. Dans le texte source, qui se présente comme un flot de caractères, l'analyse lexicale reconnaît des unités lexicales, qui sont les mots avec lesquels les phrases sont formées, et les présente à la phase suivante, l'analyse syntaxique.
Les principales sortes d'unités lexicales qu'on trouve dans les langages de programmation courants sont :
- les caractères spéciaux simples : +, =, etc. ;
- les caractères spéciaux doubles : <=, ++, etc. ;
- les mots-clés : if, while, etc. ;
- les constantes littérales : 123, -5, etc. ;
- et les identificateurs : i, vitesse_du_vent, etc.
À propos d'une unité lexicale reconnue dans le texte source on doit distinguer quatre notions importantes :
- l'unité lexicale, représentée généralement par un code conventionnel ; pour nos dix exemples +, =, <=, ++, if, while, 123, -5, i et vitesse_du_vent, ce pourrait être, respectivement(4) : PLUS, EGAL, INFEGAL, PLUSPLUS, SI, TANTQUE, NOMBRE, NOMBRE, IDENTIF, IDENTIF ;
- le lexème, qui est la chaîne de caractères correspondante. Pour les dix exemples précédents, les lexèmes correspondants sont : « + », « = », « <= », « ++ », « if », « while », « 123 », « -5 », « i » et « vitesse_du_vent » ;
- éventuellement, un attribut, qui dépend de l'unité lexicale en question, et qui la complète. Seules les dernières des dix unités précédentes ont un attribut ; pour un nombre, il s'agit de sa valeur (123, -5) ; pour un identificateur, il s'agit d'un renvoi à une table dans laquelle sont placés tous les identificateurs rencontrés (on verra cela plus loin) ;
- le modèle qui sert à spécifier l'unité lexicale. Nous verrons ci-après des moyens formels pour définir rigoureusement les modèles ; pour le moment, nous nous contenterons de descriptions informelles comme :
- pour les caractères spéciaux simples et doubles et les mots réservés, le lexème et le modèle coïncident,
- le modèle d'un nombre est « une suite de chiffres, éventuellement précédée d'un signe »,
- le modèle d'un identificateur est une suite de lettres, de chiffres et du caractère « _ », commençant par une lettre.
Outre la reconnaissance des unités lexicales, les analyseurs lexicaux assurent certaines tâches mineures comme la suppression des caractères de décoration (blancs, tabulations, fins de ligne, etc.) et celle des commentaires (généralement considérés comme ayant la même valeur qu'un blanc), l'interface avec les fonctions de lecture de caractères, à travers lesquelles le texte source est acquis, la gestion des fichiers et l'affichage des erreurs, etc.
REMARQUE : la frontière entre l'analyse lexicale et l'analyse syntaxique n'est pas fixe. D'ailleurs, l'analyse lexicale n'est pas une obligation, on peut concevoir des compilateurs dans lesquels la syntaxe est définie à partir des caractères individuels. Mais les analyseurs syntaxiques qu'il faut alors écrire sont bien plus complexes que ceux qu'on obtient en utilisant des analyseurs lexicaux pour reconnaître les mots du langage.
Simplicité et efficacité sont les raisons d'être des analyseurs lexicaux. Comme nous allons le voir, les techniques pour reconnaître les unités lexicales sont bien plus simples et efficaces que les techniques pour vérifier la syntaxe.
II-A. Expressions régulières▲
II-A-1. Définitions▲
Les expressions régulières sont une importante notation pour spécifier formellement des modèles. Pour les définir correctement il nous faut faire l'effort d'apprendre un peu de vocabulaire nouveau :
Un alphabet est un ensemble de symboles. Exemples : {0,1}, {A, C, G, T}, l'ensemble de toutes les lettres, l'ensemble des chiffres, le code ASCII, etc. On notera que les caractères blancs (c'est-à-dire les espaces, les tabulations et les marques de fin de ligne) ne font généralement pas partie des alphabets(5).
Une chaîne (on dit aussi mot) sur un alphabet Σ est une séquence finie de symboles de Σ. Exemples, respectivement relatifs aux alphabets précédents : 00011011, ACCAGTTGAAGTGGACCTTT, Bonjour, 2001. On note ε la chaîne vide, ne comportant aucun caractère.
Un langage sur un alphabet Σ est un ensemble de chaînes construites sur Σ. Exemples triviaux : ∅, le langage vide, {ε}, le langage réduit à l'unique chaîne vide. Des exemples plus intéressants (relatifs aux alphabets précédents) : l'ensemble des nombres en notation binaire, l'ensemble des chaînes ADN, l'ensemble des mots de la langue française, etc.
Si x et y sont deux chaînes, la concaténation de x et y, notée xy, est la chaîne obtenue en écrivant y immédiatement après x. Par exemple, la concaténation des chaînes anti et moine est la chaîne antimoine. Si x est une chaîne, on définit x0 = ε et, pour n > 0, xn = xn-1x = xxn-1. On a donc x1 = x, x2 = xx, x3 = xxx, etc.
Les opérations sur les langages suivantes nous serviront à définir les expressions régulières. Soient L et M deux langages, on définit :
| Dénomination | Notation | Définition |
| l'union de L et M | L U M | { x | x є L ou x є M} |
| la concaténation de L et M | LM | {xy | x є L et y є M} |
| la fermeture de Kleene de L | L* | { x1x2…xn | xi є L, n є N et n ≥ 0} |
| la fermeture positive de L | L+ | { x1x2…xn | xi є L, n є N et n > 0} |
De la définition de LM on déduit celle de Ln = LL…L.
EXEMPLES. On se donne les alphabets L = {A,B…Z, a, b… z}, ensemble des lettres, et C = {0,1… 9}, ensemble des chiffres. En considérant qu'un caractère est la même chose qu'une chaîne de longueur un, on peut voir L et C comme des langages, formés de chaînes de longueur un. Dans ces conditions :
- L U C est l'ensemble des lettres et des chiffres,
- LC est l'ensemble des chaînes formées d'une lettre suivie d'un chiffre,
- L4 est l'ensemble des chaînes de quatre lettres,
- L* est l'ensemble des chaînes faites d'un nombre quelconque de lettres ; ε en fait partie,
- C+ est l'ensemble des chaînes de chiffres comportant au moins un chiffre,
- L(L U C)* est l'ensemble des chaînes de lettres et chiffres commençant par une lettre.
Expression régulière. Soit Σ un alphabet. Une expression régulière r sur Σ est une formule qui définit un langage L(r) sur Σ, de la manière suivante :
- ε est une expression régulière qui définit le langage {ε} ;
- Si a є Σ, alors a est une expression régulière qui définit le langage(6) {a} ;
- Soient x et y deux expressions régulières, définissant les langages L(x) et L(y). Alors
- (x)|(y) est une expression régulière définissant le langage L(x) U L(y)
- (x)(y) est une expression régulière définissant le langage L(x)L(y)
- (x)* est une expression régulière définissant le langage (L(x))*
- (x) est une expression régulière définissant le langage L(x)
La dernière règle ci-dessus signifie qu'on peut encadrer une expression régulière par des parenthèses sans changer le langage défini. D'autre part, les parenthèses apparaissant dans les règles précédentes peuvent souvent être omises, en fonction des opérateurs en présence : il suffit de savoir que les opérateurs *, concaténation et |sont associatifs à gauche, et vérifient
| priorité( * ) > priorité( concaténation ) > priorité( | ) |
Ainsi, on peut écrire l'expression régulière oui au lieu de (o)(u)(i) et oui|non au lieu de (oui)|(non), mais on ne doit pas écrire oui* au lieu de (oui)*.
DÉFINITIONS RÉGULIÈRES. Les expressions régulières se construisent à partir d'autres expressions régulières ; cela amène à des expressions passablement touffues. On les allège en introduisant des définitions régulières qui permettent de donner des noms à certaines expressions en vue de leur réutilisation. On écrit donc
- d1 → r1
- d2 → r2
- …
- dn → rn
où chaque di est une chaîne sur un alphabet disjoint de Σ(7), distincte de d1, d2… di-1, et chaque ri une expression régulière sur Σ U {d1, d2… di-1}.
EXEMPLE. Voici quelques définitions régulières, et notamment celles de identificateur et nombre, qui définissent les identificateurs et les nombres du langage Pascal :
lettre → A | B | ... | Z | a | b | ... | z
chiffre → 0 | 1 | ... | 9
identificateur → lettre ( lettre | chiffre )*
chiffres → chiffre chiffre*
fraction-opt → . chiffres | ε
exposant-opt → ( E (+ | - | ε) chiffres ) | ε
nombre → chiffres fraction-opt exposant-optNOTATIONS ABRÉGÉES. Pour alléger certaines écritures, on complète la définition des expressions régulières en ajoutant les notations suivantes :
- soit x une expression régulière, définissant le langage L(x) ; alors (x)+ est une expression régulière, qui définit le langage (L(x))+,
- soit x une expression régulière, définissant le langage L(x) ; alors (x)? est une expression régulière, qui définit le langage L(x) U { ε },
- si c1, c2… ck sont des caractères, l'expression régulière c1|c2| … |ck peut se noter [c1c2 … ck],
- à l'intérieur d'une paire de crochets comme ci-dessus, l'expression c1-c2 désigne la séquence de tous les caractères c tels que c1 ≤ c ≤ c2.
Les définitions de lettre et chiffre données ci-dessus peuvent donc se réécrire :
lettre → [A-Za-z]
chiffre → [0-9]II-A-2. Ce que les expressions régulières ne savent pas faire▲
Les expressions régulières sont un outil puissant et pratique pour définir les unités lexicales, c'est-à-dire les constituants élémentaires des programmes. Mais elles se prêtent beaucoup moins bien à la spécification de constructions de niveau plus élevé, car elles deviennent rapidement d'une trop grande complexité.
De plus, on démontre qu'il y a des chaînes qu'on ne peut pas décrire par des expressions régulières. Par exemple, le langage suivant (supposé infini)
| { a, (a), ((a)), (((a)))… } |
ne peut pas être défini par des expressions régulières, car ces dernières ne permettent pas d'assurer qu'il y a dans une expression de la forme (( … ((a)) … )) autant de parenthèses ouvrantes que de parenthèses fermantes.
On dit que les expressions régulières « ne savent pas compter ».
Pour spécifier ces structures équilibrées, si importantes dans les langages de programmation (penser aux parenthèses dans les expressions arithmétiques, les crochets dans les tableaux, begin…end, {…}, if…then…, etc.)
nous ferons appel aux grammaires non contextuelles, expliquées à la section 3.1Grammaires non contextuelles.
II-B. Reconnaissance des unités lexicales▲
Nous avons vu comment spécifier les unités lexicales ; notre problème maintenant est d'écrire un programme qui les reconnaît dans le texte source. Un tel programme s'appelle un analyseur lexical.
Dans un compilateur, le principal client de l'analyseur lexical est l'analyseur syntaxique. L'interface entre ces deux analyseurs est une fonction int uniteSuivante(void)(8), qui renvoie à chaque appel l'unité lexicale suivante trouvée dans le texte source.
Cela suppose que l'analyseur lexical et l'analyseur syntaxique partagent les définitions des constantes conventionnelles définissant les unités lexicales. Si on programme en C, cela veut dire que dans les fichiers sources des deux analyseurs on a inclus un fichier d'en-tête (fichier « .h ») comportant une série de définitions comme(9) :
#define IDENTIF 1
#define NOMBRE 2
#define SI 3
#define ALORS 4
#define SINON 5
etc.Cela suppose aussi que l'analyseur lexical et l'analyseur syntaxique partagent également une variable globale contenant le lexème correspondant à la dernière unité lexicale reconnue, ainsi qu'une variable globale contenant le (ou les) attribut(s) de l'unité lexicale courante, lorsque cela est pertinent, et notamment lorsque l'unité lexicale est NOMBRE ou IDENTIF.
On se donnera, du moins dans le cadre de ce cours, quelques « règles du jeu » supplémentaires :
- l'analyseur lexical est « glouton » : chaque lexème est le plus long possible(10) ;
- seul l'analyseur lexical accède au texte source. L'analyseur syntaxique n'acquiert ses données d'entrée autrement qu'à travers la fonction uniteSuivante ;
- l'analyseur lexical acquiert le texte source un caractère à la fois. Cela est un choix que nous faisons ici ; d'autres choix auraient été possibles, mais nous verrons que les langages qui nous intéressent permettent de travailler de cette manière.
II-B-1. Diagrammes de transition▲
Pour illustrer cette section nous allons nous donner comme exemple le problème de la reconnaissance des unités lexicales INFEG, DIFF, INF, EGAL, SUPEG, SUP, IDENTIF, respectivement définies par les expressions régulières <=, <>, <, =, >=, > et lettre(lettre|chiffre)*, lettre et chiffre ayant leurs définitions déjà vues.
Les diagrammes de transition sont une étape préparatoire pour la réalisation d'un analyseur lexical. Au fur et à mesure qu'il reconnaît une unité lexicale, l'analyseur lexical passe par divers états. Ces états sont numérotés et représentés dans le diagramme par des cercles.
De chaque état e sont issues une ou plusieurs flèches étiquetées par des caractères. Une flèche étiquetée par c relie e à l'état e1 dans lequel l'analyseur passera si, alors qu'il se trouve dans l'état e, le caractère c est lu dans le texte source.
Un état particulier représente l'état initial de l'analyseur ; on le signale en en faisant l'extrémité d'une flèche étiquetée debut.
Des doubles cercles identifient les états finaux, correspondant à la reconnaissance complète d'une unité lexicale. Certains états finaux sont marqués d'une étoile : cela signifie que la reconnaissance s'est faite au prix de la lecture d'un caractère au-delà de la fin du lexème(11).
Par exemple, la figure 2 montre les diagrammes traduisant la reconnaissance des unités lexicales INFEG, DIFF, INF, EGAL, SUPEG, SUP et IDENTIF.
Un diagramme de transition est dit non déterministe lorsqu'il existe, issues d'un même état, plusieurs flèches étiquetées par le même caractère, ou bien lorsqu'il existe des flèches étiquetées par la chaîne vide ε. Dans le cas
contraire, le diagramme est dit déterministe. Il est clair que le diagramme de la figure 2 est déterministe. Seuls les diagrammes déterministes nous intéresseront dans le cadre de ce cours.
II-B-2. Analyseurs lexicaux programmés en dur ▲
Les diagrammes de transition sont une aide importante pour l'écriture d'analyseurs lexicaux. Par exemple, à partir du diagramme de la figure 2 on peut obtenir rapidement un analyseur lexical reconnaissant les unités INFEG, DIFF, INF, EGAL, SUPEG, SUP et IDENTIF.
Auparavant, nous apportons une légère modification à nos diagrammes de transition, afin de permettre que les unités lexicales soient séparées par un ou plusieurs blancs(12). La figure 3 montre le (début du) diagramme modifié(13).
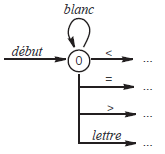
Et voici le programme obtenu :
int uniteSuivante(void) {
char c;
c = lireCar(); /* etat = 0 */
while (estBlanc(c))
c = lireCar();
if (c == '<') {
c = lireCar(); /* etat = 1 */
if (c == '=')
return INFEG; /* etat = 2 */
else if (c == '>')
return DIFF; /* etat = 3 */
else {
delireCar(c); /* etat = 4 */
return INF;
}
}
else if (c == '=')
return EGAL; /* etat = 5 */
else if (c == '>') {
c = lireCar(); /* etat = 6 */
if (c == '=')
return SUPEG; /* etat = 7 */
else {
delireCar(c); /* etat = 8 */
return SUP;
}
}
else if (estLettre(c)) {
lonLex = 0; /* etat = 9 */
lexeme[lonLex++] = c;
c = lireCar();
while (estLettre(c) || estChiffre(c)) {
lexeme[lonLex++] = c;
c = lireCar();
}
delireCar(c); /* etat = 10 */
return IDENTIF;
}
else {
delireCar(c);
return NEANT; /* ou bien donner une erreur */
}
}Dans le programme précédent on utilise des fonctions auxiliaires, dont voici une version simple :
int estBlanc(char c) {
return c == ' ' || c == '\t' || c == '\n';
}
int estLettre(char c) {
return 'A' <= c && c <= 'Z' || 'a' <= c && c <= 'z';
}
int estChiffre(char c) {
return '0' <= c && c <= '9';
}NOTE. On peut augmenter l'efficacité de ces fonctions, au détriment de leur sécurité d'utilisation, en en faisant des macros :
#define estBlanc(c) ((c) == ' ' || (c) == '\t' || (c) == '\n')
#define estLettre(c) ('A' <= (c) && (c) <= 'Z' || 'a' <= (c) && (c) <= 'z')
#define estChiffre(c) ('0' <= (c) && (c) <= '9')Il y plusieurs manières de prendre en charge la restitution d'un caractère lu en trop (notre fonction delireCar).
Si on dispose de la bibliothèque standard C on peut utiliser la fonction ungetc :
void delireCar(char c) {
ungetc(c, stdin);
}
char lireCar(void) {
return getc(stdin);
}Une autre manière de faire permet de se passer de la fonction ungetc. Pour cela, on gère une variable globale contenant, quand il y a lieu, le caractère lu en trop (il n'y a jamais plus d'un caractère lu en trop). Déclaration :
int carEnAvance = -1;avec cela nos deux fonctions deviennent
void delireCar(char c) {
carEnAvance = c;
}
char lireCar(void) {
char r;
if (carEnAvance >= 0) {
r = carEnAvance;
carEnAvance = -1;
}
else
r = getc(stdin);
return r;
}RECONNAISSANCE DES MOTS RÉSERVÉS. Les mots réservés appartiennent au langage défini par l'expression régulière lettre(lettre|chiffre)*, tout comme les identificateurs. Leur reconnaissance peut donc se traiter de deux manières :
- soit on incorpore les mots réservés aux diagrammes de transition, ce qui permet d'obtenir un analyseur très efficace, mais au prix d'un travail de programmation plus important, car les diagrammes de transition deviennent très volumineux(14) ;
- soit on laisse l'analyseur traiter de la même manière les mots réservés et les identificateurs puis, quand la reconnaissance d'un « identificateur-ou-mot-réservé » est terminée, on recherche le lexème dans une table pour déterminer s'il s'agit d'un identificateur ou d'un mot réservé.
Dans les analyseurs lexicaux « en dur » on utilise souvent la deuxième méthode, plus facile à programmer.
On se donne donc une table de mots réservés :
struct {
char *lexeme;
int uniteLexicale;
} motRes[] = {
{ "si", SI },
{ "alors", ALORS },
{ "sinon", SINON },
...
};
int nbMotRes = sizeof motRes / sizeof motRes[0];puis on modifie de la manière suivante la partie concernant les identificateurs de la fonction uniteSuivante :
...
else if (estLettre(c)) {
lonLex = 0; /* etat = 9 */
lexeme[lonLex++] = c;
c = lireCar();
while (estLettre(c) || estChiffre(c)) {
lexeme[lonLex++] = c;
c = lireCar();
}
delireCar(c); /* etat = 10 */
lexeme[lonLex] = '\0';
for (i = 0; i < nbMotRes; i++)
if (strcmp(lexeme, motRes[i].lexeme) == 0)
return motRes[i].uniteLexicale;
return IDENTIF;
}
...II-B-3. Automates finis▲
Un automate fini est défini par la donnée de
- un ensemble fini d'états E ;
- un ensemble fini de symboles (ou alphabet) d'entrée Σ ;
- une fonction de transition, transit : E x Σ → E ;
- un état ε0 distingué, appelé état initial ;
- un ensemble d'états F, appelés états d'acceptation ou états finaux.
Un automate peut être représenté graphiquement par un graphe où les états sont figurés par des cercles (les états finaux par des cercles doubles) et la fonction de transition par des flèches étiquetées par des caractères : si transit(e1, c) = e2 alors le graphe a une flèche étiquetée par le caractère c, issue de e1 et aboutissant à e2.
Un tel graphe est exactement ce que nous avons appelé diagramme de transition à la section 2.2.1Diagrammes de transition (voir la figure 2). Si on en reparle ici c'est qu'on peut en déduire un autre style d'analyseur lexical, assez différent de ce que nous avons appelé analyseur programmé en dur.
On dit qu'un automate fini accepte une chaîne d'entrée s = c1c2 … ck si, et seulement si, il existe dans le graphe de transition un chemin joignant l'état initial e0 à un certain état final ek, composé de k flèches étiquetées par les caractères c1, c2… ck.
Pour transformer un automate fini en un analyseur lexical il suffira donc d'associer une unité lexicale à chaque état final et de faire en sorte que l'acceptation d'une chaîne produise comme résultat l'unité lexicale associée à l'état final en question.
Autrement dit, pour programmer un analyseur il suffira maintenant d'implémenter la fonction transitce qui, puisqu'elle est définie sur des ensembles finis, pourra se faire par une table à double entrée. Pour les diagrammes des figures 2 et 3 cela donne la table suivante (les états finaux sont indiqués en gras, leurs lignes ont été supprimées) :
| ' ' | '\t' | '\n' | '<' | '=' | '>' | lettre | chiffre | autre | |
| 0 | 0 | 0 | 0 | 1 | 5 | 6 | 9 | erreur | erreur |
| 1 | 4* | 4* | 4* | 4* | 2 | 3 | 4* | 4* | 4* |
| 6 | 8* | 8* | 8* | 8* | 7 | 8* | 8* | 8* | 8* |
| 9 | 10* | 10* | 10* | 10* | 10* | 10* | 9 | 9 | 10* |
On obtiendra un analyseur peut-être plus encombrant que dans la première manière, mais certainement plus rapide puisque l'essentiel du travail de l'analyseur se réduira à répéter « bêtement » l'action etat = transit[etat][lireCar()] jusqu'à tomber sur un état final. Voici ce programme :
#define NBR_ETATS ...
#define NBR_CARS 256
int transit[NBR_ETATS][NBR_CARS];
int final[NBR_ETATS + 1];
int uniteSuivante(void) {
char caractere;
int etat = etatInitial;
while ( ! final[etat]) {
caractere = lireCar();
etat = transit[etat][caractere];
}
if (final[etat] < 0)
delireCar(caractere);
return abs(final[etat]) - 1;
}Notre tablefinalement, indexé par les états, est défini par
- final[e] = 0 si e n'est pas un état final (vu comme un booléen, final[e] est faux),
- final[e] = U + 1 si e est final, sans étoile et associé à l'unité lexicale U (en tant que booléen, final[e] est vrai, car les unités lexicales sont numérotées au moins à partir de zéro),
- final[e] = ¡(U + 1) si e est final, étoilé et associé à l'unité lexicale U (en tant que booléen, final[e] est encore vrai).
Enfin, voici comment les tableaux transit et final devraient être initialisés pour correspondre aux diagrammes des figures 2 et 3(15) :
void initialiser(void) {
int i, j;
for (i = 0; i < NBR_ETATS; i++) final[i] = 0;
final[ 2] = INFEG + 1;
final[ 3] = DIFF + 1;
final[ 4] = - (INF + 1);
final[ 5] = EGAL + 1;
final[ 7] = SUPEG + 1;
final[ 8] = - (SUP + 1);
final[10] = - (IDENTIF + 1);
final[NBR_ETATS] = ERREUR + 1;
for (i = 0; i < NBR_ETATS; i++)
for (j = 0; j < NBR_CARS; j++)
transit[i][j] = NBR_ETATS;
transit[0][' '] = 0;
transit[0]['\t'] = 0;
transit[0]['\n'] = 0;
transit[0]['<'] = 1;
transit[0]['='] = 5;
transit[0]['>'] = 6;
for (j = 'A'; j <= 'Z'; j++) transit[0][j] = 9;
for (j = 'a'; j <= 'z'; j++) transit[0][j] = 9;
for (j = 0; j < NBR_CARS; j++) transit[1][j] = 4;
transit[1]['='] = 2;
transit[1]['>'] = 3;
for (j = 0; j < NBR_CARS; j++) transit[6][j] = 8;
transit[6]['='] = 7;
for (j = 0; j < NBR_CARS; j++) transit[9][j] = 10;
for (j = 'A'; j <= 'Z'; j++) transit[9][j] = 9;
for (j = 'a'; j <= 'z'; j++) transit[9][j] = 9;
for (j = '0'; j <= '9'; j++) transit[9][j] = 9;
}II-C. Lex, un générateur d'analyseurs lexicaux▲
Les analyseurs lexicaux basés sur des tables de transitions sont les plus efficaces… une fois la table de transition construite. Or, la construction de cette table est une opération longue et délicate.
Le programme lex(16)fait cette construction automatiquement : il prend en entrée un ensemble d'expressions régulières et produit en sortie le texte source d'un programme C qui, une fois compilé, est l'analyseur lexical correspondant au langage défini par les expressions régulières en question.
Plus précisément (voyez la figure 4), lex produit un fichier source C, nommé lex.yy.c, contenant la définition de la fonction int yytext(void), qui est l'exacte homologue de notre fonction uniteSuivante de la section 2.2.2Analyseurs lexicaux programmés en dur : un programme appelle cette fonction et elle renvoie une unité lexicale reconnue dans le texte source.
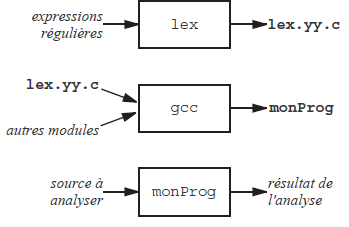
II-C-1. Structure d'un fichier source pour lex▲
En lisant cette section, souvenez-vous de ceci : lex écrit un fichier source C. Ce fichier est fait de trois sortes d'ingrédients :
- des tables garnies de valeurs calculées à partir des expressions régulières fournies ;
- des morceaux de code C invariable, et notamment le « moteur » de l'automate, c'est-à-dire la boucle qui répète inlassablement etat ← transit (etat; caractere) ;
- des morceaux de code C, trouvés dans le fichier source lex et recopiés tels quels, à l'endroit voulu, dans le fichier produit.
Un fichier source pour lex doit avoir un nom qui se termine par « .l ». Il est fait de trois sections, délimitées par deux lignes réduites(17) au symbole « %% » :
%{
déclarations pour le compilateur C
%}
définitions régulières
%%
règles
%%
fonctions C supplémentairesLa partie « déclarations pour le compilateur C » et les symboles « %{ » et « %} » qui l'encadrent peuvent être omis.
Quand elle est présente, cette partie se compose de déclarations qui seront simplement recopiées au début du fichier produit. En plus d'autres choses, on trouve souvent ici une directive #include qui produit l'inclusion du fichier « .h » contenant les définitions des codes conventionnels des unités lexicales (INFEG, INF, EGAL, etc.).
La troisième section « fonctions C supplémentaires » peut être absente également (le symbole « %% » qui la sépare de la deuxième section peut alors être omis). Cette section se compose de fonctions C qui seront simplement recopiées à la fin du fichier produit.
DÉFINITIONS RÉGULIÈRES. Les définitions régulières sont de la forme identificateur expressionRégulière où identificateur est écrit au début de la ligne (pas de blancs avant) et séparé de expressionRégulière par des blancs. Exemples :
lettre [A-Za-z]
chiffre [0-9]Les identificateurs ainsi définis peuvent être utilisés dans les règles et dans les définitions subséquentes ; il faut alors les encadrer par des accolades. Exemples :
lettre [A-Za-z]
chiffre [0-9]
alphanum {lettre}|{chiffre}
%%
{lettre}{alphanum}* { return IDENTIF; }
{chiffre}+("."{chiffre}+)? { return NOMBRE; }Règles. Les règles sont de la forme
expressionRégulière { action }où expressionRégulière est écrit au début de la ligne (pas de blancs avant) ; action est un morceau de code source C, qui sera recopié tel quel, au bon endroit, dans la fonction yylex. Exemples :
if { return SI; }
then { return ALORS; }
else { return SINON; }
. . .
{lettre}{alphanum}* { return IDENTIF; }La règle
expressionRégulière { action }signifie « à la fin de la reconnaissance d'une chaîne du langage défini par expressionRégulière exécutez action ». Le traitement par lex d'une telle règle consiste donc à recopier l'action indiquée à un certain endroit de la fonction yylex(18). Dans les exemples ci-dessus, les actions étant toutes de la forme « return unite », leur signification est claire : quand une chaîne du texte source est reconnue, la fonction yylex se termine en rendant comme résultat l'unité lexicale reconnue. Il faudra appeler de nouveau cette fonction pour que l'analyse du texte source reprenne.
À la fin de la reconnaissance d'une unité lexicale la chaîne acceptée est la valeur de la variable yytext, de type chaîne de caractères(19). Un caractère nul indique la fin de cette chaîne ; de plus, la variable entière yylen donne le nombre de ses caractères. Par exemple, la règle suivante reconnaît les nombres entiers et en calcule la valeur dans une variable yylval :
(+|-)?[0-9]+ { yylval = atoi(yytext); return NOMBRE; }EXPRESSIONS RÉGULIÈRES. Les expressions régulières acceptées par lex sont une extension de celles définies à la section 2.1Expressions régulières. Les métacaractères précédemment introduits, c'est-à-dire (, ), |, *, +, ?, [, ] et -à l'intérieur des crochets, sont légitimes dans lex et y ont le même sens. En outre, on dispose de ceci (liste non exhaustive) :
- un point . signifie un caractère quelconque, différent de la marque de fin de ligne ;
- on peut encadrer par des guillemets un caractère ou une chaîne, pour éviter que les métacaractères qui s'y trouvent soient interprétés comme tels. Par exemple, « . » signifie le caractère « . » (et non pas un caractère quelconque), « " signifie un blanc, »[a-z]" signifie la chaîne [a-z], etc.
D'autre part, on peut sans inconvénient encadrer par des guillemets un caractère ou une chaîne qui n'en avaient pas besoin ; - l'expression [^caractères] signifie : tout caractère n'appartenant pas à l'ensemble défini par [caractères] ;
- l'expression « ^expressionRégulière » signifie : toute chaîne reconnue par expressionRégulière à la condition qu'elle soit au début d'une ligne ;
- l'expression « expressionRégulière$ » signifie : toute chaîne reconnue par expressionRégulière à la condition qu'elle soit à la fin d'une ligne.
Il faut être très soigneux en écrivant les définitions et les règles dans le fichier source lex. En effet, tout texte qui n'est pas exactement à sa place (par exemple une définition ou une règle qui ne commencent pas au début de la ligne) sera recopié dans le fichier produit par lex. C'est un comportement voulu, parfois utile, mais qui peut conduire à des situations confuses.
ECHO DU TEXTE ANALYSÉ. L'analyseur lexical produit par lex prend son texte source sur l'entrée standard(20) et l'écrit, avec certaines modifications, sur la sortie standard. Plus précisément :
- tous les caractères qui ne font partie d'aucune chaîne reconnue sont recopiés sur la sortie standard (ils « traversent » l'analyseur lexical sans en être affectés) ;
- une chaîne acceptée au titre d'une expression régulière n'est pas recopiée sur la sortie standard.
Bien entendu, pour avoir les chaînes acceptées dans le texte écrit par l'analyseur il suffit de le prévoir dans l'action correspondante. Par exemple, la règle suivante reconnaît les identificateurs et fait en sorte qu'ils figurent dans le texte sorti :
[A-Za-z][A-Za-z0-9]* { printf("%s", yytext); return IDENTIF; }Le texte printf(« %s », yytext) apparaît très fréquemment dans les actions. On peut l'abréger en ECHO :
[A-Za-z][A-Za-z0-9]* { ECHO; return IDENTIF; }II-C-2. Un exemple complet▲
Voici le texte source pour créer l'analyseur lexical d'un langage comportant les nombres et les identificateurs définis comme d'habitude, les mots réservés si, alors, sinon, tantque, faire et rendre et les opérateurs doubles ==, !=, <= et >=. Les unités lexicales correspondantes sont respectivement représentées par les constantes conventionnelles IDENTIF, NOMBRE, SI, ALORS, SINON, TANTQUE, FAIRE, RENDRE, EGAL, DIFF, INFEG, SUPEG, définies dans le fichier unitesLexicales.h.
Pour les opérateurs simples, on décide que tout caractère non reconnu par une autre expression régulière est une unité lexicale, et qu'elle est représentée par son propre code ASCII(21). Pour éviter des collisions entre ces codes ASCII et les unités lexicales nommées, on donne à ces dernières des valeurs supérieures à 255.
#define IDENTIF 256
#define NOMBRE 257
#define SI 258
#define ALORS 259
#define SINON 260
#define TANTQUE 261
#define FAIRE 262
#define RENDRE 263
#define EGAL 264
#define DIFF 265
#define INFEG 266
#define SUPEG 267
extern int valNombre;
extern char valIdentif[];%{
#include "unitesLexicales.h"
%}
chiffre [0-9]
lettre [A-Za-z]
%%
[" "\t\n] { ECHO; /* rien */ }
{chiffre}+ { ECHO; valNombre = atoi(yytext); return NOMBRE; };
si { ECHO; return SI; }
alors { ECHO; return ALORS; }
sinon { ECHO; return SINON; }
tantque { ECHO; return TANTQUE; }
fairerendre { ECHO; return FAIRE; }
{lettre}({lettre}|{chiffre})* {
ECHO; strcpy(valIdentif, yytext); return IDENTIF; }
"==" { ECHO; return EGAL; }
"!=" { ECHO; return DIFF; }
"<=" { ECHO; return INFEG; }
">=" { ECHO; return SUPEG; }
. { ECHO; return yytext[0]; }
%%
int valNombre;
char valIdentif[256];
int yywrap(void) {
return 1;
}#include <stdio.h>
#include "unitesLexicales.h"
int main(void) {
int unite;
do {
unite = yylex();
printf(" (unite: %d", unite);
if (unite == NOMBRE)
printf(" val: %d", valNombre);
else if (unite == IDENTIF)
printf(" '%s'", valIdentif);
printf(")\n");
} while (unite != 0);
return 0;
}si x == 123 alors
y = 0;Création d'un exécutable et essai sur le texte précédent (rappelons que lex s'appelle flex dans le monde Linux) ; $ est le prompt du système :
$ flex analex.l
$ gcc lex.yy.c principal.c -o monprog
$ monprog < essai.txt
si (unite: 258)
x (unite: 256 'x')
== (unite: 264)
123 (unite: 257 val: 123)
alors (unite: 259)
y (unite: 256 'y')
= (unite: 61)
0 (unite: 257 0)
; (unite: 59)
$NOTE. La fonction yywrap qui apparaît dans notre fichier source pour lex est appelée lorsque l'analyseur rencontre la fin du fichier à analyser(22). Outre d'éventuelles actions utiles dans telle ou telle application particulière, cette fonction doit rendre une valeur non nulle pour indiquer que le flot d'entrée est définitivement épuisé, ou bien ouvrir un autre flot d'entrée.
II-C-3. Autres utilisations de lex▲
Ce que le programme généré par lex fait nécessairement, c'est reconnaître les chaînes du langage défini par les expressions régulières données. Quand une telle reconnaissance est accomplie, on n'est pas obligé de renvoyer une unité lexicale pour signaler la chose ; on peut notamment déclencher l'action qu'on veut et ne pas retourner à la fonction appelante. Cela permet d'utiliser lex pour effectuer d'autres sortes de programmes que des analyseurs lexicaux.
Par exemple, supposons que nous disposons de textes contenant des indications de prix en francs. Voici comment obtenir rapidement un programme qui met tous ces prix en euros :
%%
[0-9]+("."[0-9]*)?[" "\t\n]*F(rancs|".")?[" "\t\n] {
printf("%.2f EUR ", atof(yytext) / 6.55957); }
%%
int yywrap(void) {
return 1;
}
int main(void) {
yylex();
}Le programme précédent exploite le fait que tous les caractères qui ne font pas partie d'une chaîne reconnue sont recopiés sur la sortie ; ainsi, la plupart des caractères du texte donné seront recopiés tels quels. Les chaînes reconnues sont définies par l'expression régulière
[0-9]+("."[0-9]*)?[" "\t\n]*F(rancs|".")?[" "\t\n]Cette expression se lit, successivement :
- une suite d'au moins un chiffre ;
- éventuellement, un point suivi d'un nombre quelconque de chiffres ;
- éventuellement, un nombre quelconque de blancs (espaces, tabulations, fins de ligne) ;
- un F majuscule obligatoire ;
- éventuellement, la chaîne rancs ou un point (ainsi, « F », « F. » et « Francs » sont tous trois acceptés) ;
- enfin, un blanc obligatoire.
Lorsqu'une chaîne s'accordant à cette syntaxe est reconnue, comme « 99.50 Francs », la fonction atof obtient la valeur que [le début de] cette chaîne représente. Il suffit alors de mettre dans le texte de sortie le résultat de la division de cette valeur par le taux adéquat ; soit, ici, « 15.17 EUR ».



