III. Analyse syntaxique▲
III-A. Grammaires non contextuelles▲
Les langages de programmation sont souvent définis par des règles récursives, comme : « on a une expression en écrivant successivement un terme, '+' et une expression » ou « on obtient une instruction en écrivant à la suite si, une expression, alors, une instruction et, éventuellement, sinon et une instruction ». Les grammaires non contextuelles sont un formalisme particulièrement bien adapté à la description de telles règles.
III-A-1. Définitions▲
Une grammaire non contextuelle, on dit parfois grammaire BNF (pour Backus-Naur form(23)), est un quadruplet G = (VT , VN, S0, P) formé de
- un ensemble VT de symboles terminaux ;
- un ensemble VN de symboles non terminaux ;
- un symbole S0 є VN particulier, appelé symbole de départ ou axiome ;
- un ensemble P de productions, qui sont des règles de la forme
S → S1S2 … Sk avec S є VN et Si є VN U VT.
Compte tenu de l'usage que nous en faisons dans le cadre de l'écriture de compilateurs, nous pouvons expliquer ces éléments de la manière suivante :
- Les symboles terminaux sont les symboles élémentaires qui constituent les chaînes du langage, les phrases. Ce sont donc les unités lexicales, extraites du texte source par l'analyseur lexical (il faut se rappeler que l'analyseur syntaxique ne connaît pas les caractères dont le texte source est fait, il ne voit ce dernier que comme une suite d'unités lexicales).
- Les symboles non terminaux sont des variables syntaxiques désignant des ensembles de chaînes de symboles terminaux.
- Le symbole de départ est un symbole non terminal particulier qui désigne le langage en son entier.
- Les productions peuvent être interprétées de deux manières :
- comme des règles d'écriture (on dit plutôt de réécriture), permettant d'engendrer toutes les chaînes correctes. De ce point de vue, la production S → S1S2 … Sk se lit « pour produire un S correct [sous-entendu : de toutes les manières possibles] il fait produire un S1 [de toutes les manières possibles] » suivi d'un S2 [de toutes les manières possibles] suivi d'un… suivi d'un Sk [de toutes les manières possibles],
- comme des règles d'analyse, on dit aussi reconnaissance. La production S → S1S2 … Sk se lit alors « pour reconnaître un S, dans une suite de terminaux donnée, il faut reconnaître un S1 suivi d'un S2 suivi d'un… suivi d'un Sk ».
La définition d'une grammaire devrait donc commencer par l'énumération des ensembles VT et VN. En pratique on se limite à donner la liste des productions, avec une convention typographique pour distinguer les symboles terminaux des symboles non terminaux, et on convient que :
- VT est l'ensemble de tous les symboles terminaux apparaissant dans les productions ;
- VN est l'ensemble de tous les symboles non terminaux apparaissant dans les productions ;
- le symbole de départ est le membre gauche de la première production.
En outre, on allège les notations en décidant que si plusieurs productions ont le même membre gauche
- S → S1,1 S1,2 … S1,k1
- S → S2,1 S2,2 … S2,k2
- . . .
- S → Sn,1 Sn,2 … Sn,kn
alors on peut les noter simplement
- S → S1,1 S1,2 … S1,k1 | S2,1 S2,2 … S2,k2 | … | Sn,1 Sn,2 … Sn,kn
Dans les exemples de ce document, la convention typographique sera la suivante :
- une chaîne en italique représente un symbole non terminal ;
- une chaîne en caractères_télétype ou « entre guillemets », représente un symbole terminal.
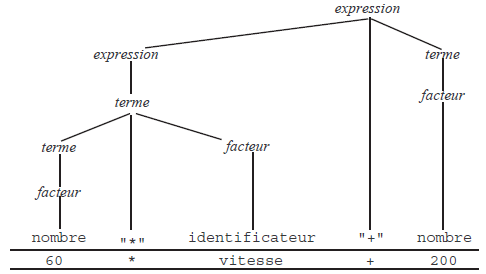
À titre d'exemple, voici la grammaire G1 définissant le langage dont les chaînes sont les expressions arithmétiques formées avec des nombres, des identificateurs et les deux opérateurs + et *, comme 60 * vitesse + 200 . Suivant notre convention, les symboles non terminaux sont expression, terme et facteur ; le symbole de départ est expression :
expression → expression "+" terme | terme
terme → terme "*" facteur | facteur (G1)
facteur → nombre | identificateur | "(" expression ")"III-A-2. Dérivations et arbres de dérivation▲
Dérivation. Le processus par lequel une grammaire définit un langage s'appelle dérivation. Il peut être formalisé de la manière suivante :
Soit G = (VT , VN, S0, P) une grammaire non contextuelle, A ∈ VN un symbole non terminal et γ ∈ (VT U VN)* une suite de symboles, tels qu'il existe dans P une production A → γ. Quelles que soient les suites de symboles α et β, on dit que αAβ se dérive en une étape en la suite αγβ ce qui s'écrit
| αAβ => αγβ |
Cette définition justifie la dénomination grammaire non contextuelle (on dit aussi grammaire indépendante du contexte ou context free). En effet, dans la suite αAβ les chaînes α et β sont le contexte du symbole A. Ce que cette définition dit, c'est que le symbole A se réécrit dans la chaîne γ quel que soit le contexte α, β dans lequel A apparaît.
Si α0 ⇒ α1 ⇒ … ⇒ αn on dit que α0 se dérive en αn en n étapes, et on écrit
| α0 |
Enfin, si α se dérive en β en un nombre quelconque, éventuellement nul, d'étapes on dit simplement que α se dérive en β et on écrit
| α |
Soit G = {VT, VN, S0, P} une grammaire non contextuelle ; le langage engendré par G est l'ensemble des chaînes de symboles terminaux qui dérivent de S0 :
| L(G) = { w ∈ VT* | S0 |
Si w ∈ L(G) on dit que w est une phrase de G. Plus généralement, si �� ∈ (VT U VN)* est tel que S0 ![]() α alors on dit que α est une proto-phrase de G. Une proto-phrase dont tous les symboles sont terminaux est une phrase.
α alors on dit que α est une proto-phrase de G. Une proto-phrase dont tous les symboles sont terminaux est une phrase.
Par exemple, soit encore la grammaire G1 :
expression → expression "+" terme | terme
terme → terme "*" facteur | facteur (G1)
facteur → nombre | identificateur | "(" expression ")"et considérons la chaîne « 60 * vitesse + 200 » qui, une fois lue par l'analyseur lexical, se présente ainsi : w = ( nombre « * » identificateur « + » nombre ). Nous avons expression ![]() w, c'est-à-dire w є L(G1) ; en effet, nous pouvons exhiber la suite de dérivations en une étape :
w, c'est-à-dire w є L(G1) ; en effet, nous pouvons exhiber la suite de dérivations en une étape :
expression => expression "+" terme
=> terme "+" terme
=> terme "*" facteur "+" terme
=> facteur "*" facteur "+" terme
=> nombre "*" facteur "+" terme
=> nombre "*" identificateur "+" terme
=> nombre "*" identificateur "+" facteur
=> nombre "*" identificateur "+" nombreDÉRIVATION GAUCHE. La dérivation précédente est appelée une dérivation gauche car elle est entièrement composée de dérivations en une étape dans lesquelles à chaque fois c'est le non-terminal le plus à gauche qui est réécrit. On peut définir de même une dérivation droite où, à chaque étape, c'est le non-terminal le plus à droite qui est réécrit.
ARBRE DE DÉRIVATION. Soit w une chaîne de symboles terminaux du langage L(G) ; il existe donc une dérivation telle que S0 ![]() w. Cette dérivation peut être représentée graphiquement par un arbre, appelé arbre de dérivation, défini de la manière suivante :
w. Cette dérivation peut être représentée graphiquement par un arbre, appelé arbre de dérivation, défini de la manière suivante :
- la racine de l'arbre est le symbole de départ ;
- les nœuds intérieurs sont étiquetés par des symboles non terminaux ;
- si un nœud intérieur e est étiqueté par le symbole S et si la production S → S1S2 … Sk a été utilisée pour dériver S alors les fils de e sont des nœuds étiquetés, de la gauche vers la droite, par S1, S2… Sk ;
- les feuilles sont étiquetées par des symboles terminaux et, si on allonge verticalement les branches de l'arbre (sans les croiser) de telle manière que les feuilles soient toutes à la même hauteur, alors, lues de la gauche vers la droite, elles constituent la chaîne w.
Par exemple, la figure 5 montre l'arbre de dérivation représentant la dérivation donnée en exemple ci-dessus.
On notera que l'ordre des dérivations (gauche, droite) ne se voit pas sur l'arbre.
III-A-3. Qualités des grammaires en vue des analyseurs▲
Étant donnée une grammaire G = {VT, VN, S0, P}, faire l'analyse syntaxique d'une chaîne w ∈ VT* c'est répondre à la question « w appartient-elle au langage L(G) ? ». Parlant strictement, un analyseur syntaxique est donc un programme qui n'extrait aucune information de la chaîne analysée, il ne fait qu'accepter (par défaut) ou rejeter (en annonçant une erreur de syntaxe) cette chaîne.
En réalité on ne peut pas empêcher les analyseurs d'en faire un peu plus car, pour prouver que w ∈ L(G) il faut exhiber une dérivation S0 ![]() w, c'est-à-dire construire un arbre de dérivation dont la liste des feuilles est w. Or, cet arbre de dérivation est déjà une première information extraite de la chaîne source, un début de « compréhension » de ce que le texte signifie.
w, c'est-à-dire construire un arbre de dérivation dont la liste des feuilles est w. Or, cet arbre de dérivation est déjà une première information extraite de la chaîne source, un début de « compréhension » de ce que le texte signifie.
Nous examinons ici des qualités qu'une grammaire doit avoir et des défauts dont elle doit être exempte pour que la construction de l'arbre de dérivation de toute chaîne du langage soit possible et utile.
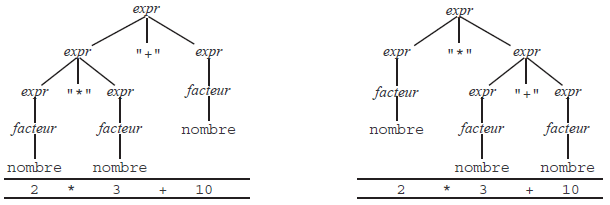
GRAMMAIRES AMBIGUËS. Une grammaire est ambiguë s'il existe plusieurs dérivations gauches différentes pour une même chaîne de terminaux. Par exemple, la grammaire G2 suivante est ambiguë :
expression → expression "+" expression | expression "*" expression | facteur (G2)
facteur → nombre | identificateur | "(" expression ")"En effet, la figure 6 montre deux arbres de dérivation distincts pour la chaîne « 2 * 3 + 10 ». Ils correspondent aux deux dérivations gauches distinctes :
expression => expression "+" expression => expression "*" expression "+" expression
=> facteur "*" expression "+" expression => nombre "*" expression "+" expression
=> nombre "*" facteur "+" expression => nombre "*" nombre "+" expression
=> nombre "*" nombre "+" facteur => nombre "*" nombre "+" nombreet
expression => expression "*" expression => facteur "*" expression
=> nombre "*" expression => nombre "*" expression "+" expression
=> nombre "*" facteur "+" expression => nombre "*" nombre "+" expression
=> nombre "*" nombre "+" facteur => nombre "*" nombre "+" nombreDeux grammaires sont dites équivalentes si elles engendrent le même langage. Il est souvent possible de remplacer une grammaire ambiguë par une grammaire non ambiguë équivalente, mais il n'y a pas une méthode générale pour cela. Par exemple, la grammaire G1 est non ambiguë et équivalente à la grammaire G2 ci-dessus.
GRAMMAIRES RÉCURSIVES À GAUCHE. Une grammaire est récursive à gauche s'il existe un non-terminal A et une dérivation de la forme A ![]() Aα, où α est une chaîne quelconque. Cas particulier, on dit qu'on a une récursivité à gauche simple si la grammaire possède une production de la forme A → Aα.
Aα, où α est une chaîne quelconque. Cas particulier, on dit qu'on a une récursivité à gauche simple si la grammaire possède une production de la forme A → Aα.
La récursivité à gauche ne rend pas une grammaire ambiguë, mais empêche l'écriture d'analyseurs pour cette grammaire, du moins des analyseurs descendants(24).
Par exemple, la grammaire G1 de la section 3.1.1Définitions est récursive à gauche, et même simplement :
expression → expression "+" terme | terme
terme → terme "*" facteur | facteur (G1)
facteur → nombre | identificateur | "(" expression ")"Il existe une méthode pour obtenir une grammaire non récursive à gauche équivalente à une grammaire donnée. Dans le cas de la récursivité à gauche simple, cela consiste à remplacer une production telle que
A → Aα | βpar les deux productions(25)
A → βA0
A0 → αA0 | εEn appliquant ce procédé à la grammaire G1 on obtient la grammaire G3 suivante :
expression → terme fin expression
fin expression → "+" terme fin expression | ε
terme → facteur fin terme (G3)
fin terme → "*" facteur fin terme | ε
facteur → nombre | identificateur | "(" expression ")"À PROPOS DES ε -PRODUCTIONS. La transformation de grammaire montrée ci-dessus a introduit des productions avec un membre droit vide, ou ε-productions. Si on ne prend pas de disposition particulière, on aura un problème pour l'écriture d'un analyseur, puisqu'une production telle que
fin expression → "+" terme fin expression | εimpliquera notamment que « une manière de reconnaître une fin expression consiste à ne rien reconnaître », ce qui est possible quelle que soit la chaîne d'entrée ; ainsi, notre grammaire semble devenir ambiguë. On résout ce problème en imposant aux analyseurs que nous écrirons la règle de comportement suivante : dans la dérivation d'un non-terminal, une ε-production ne peut être choisie que lorsqu'aucune autre production n'est applicable.
Dans l'exemple précédent, cela donne : si la chaîne d'entrée commence par + alors on doit nécessairement choisir la première production.
FACTORISATION À GAUCHE. Nous cherchons à écrire des analyseurs prédictifs. Cela veut dire qu'à tout moment le choix entre productions qui ont le même membre gauche doit pouvoir se faire, sans risque d'erreur, en comparant le symbole courant de la chaîne à analyser avec les symboles susceptibles de commencer les dérivations des membres droits des productions en compétition.
Une grammaire contenant des productions comme
A → αβ1 | αβ2viole ce principe car lorsqu'il faut choisir entre les productions A → αβ1 et A → αβ2 le symbole courant est un de ceux qui peuvent commencer une dérivation de α, et on ne peut pas choisir à coup sûr entre αβ1 et αβ2.
Une transformation simple, appelée factorisation à gauche, corrige ce défaut (si les symboles susceptibles de commencer une réécriture de β1 sont distincts de ceux pouvant commencer une réécriture de β2) :
A → αA0
A0 → β1 | β2Exemple classique. Les grammaires de la plupart des langages de programmation définissent ainsi l'instruction conditionnelle :
instr si → si expr alors instr | si expr alors instr sinon instrPour avoir un analyseur prédictif, il faudra opérer une factorisation à gauche :
instr_si → si expr alors instr in_instr_si
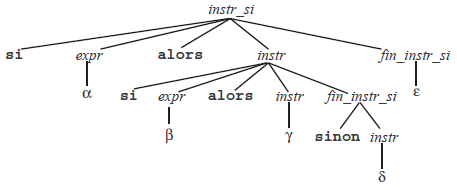
fin_instr_si → sinon instr | εComme précédemment, l'apparition d'une ε-production semble rendre ambiguë la grammaire. Plus précisément, la question suivante se pose : n'y a-t-il pas deux arbres de dérivation possibles pour la chaîne(26) :
| si α alors si β alors γ sinon δ |
Nous l'avons déjà dit, on lève cette ambiguïté en imposant que la ε-production ne peut être choisie que si aucune autre production n'est applicable. Autrement dit, si, au moment où l'analyseur doit dériver le non-terminal fin_instr_si, la chaîne d'entrée commence par le terminal sinon, alors la production « fin_instr_si → sinon instr » doit être appliquée. La figure 7 montre l'arbre de dérivation obtenu pour la chaîne précédente.
III-A-4. Ce que les grammaires non contextuelles ne savent pas faire▲
Les grammaires non contextuelles sont un outil puissant, en tout cas plus puissant que les expressions régulières, mais il existe des langages (pratiquement tous les langages de programmation, excusez du peu… !) qu'elles ne peuvent pas décrire complètement.
On démontre par exemple que le langage L = {wcw | w є (a|b)*}, où a, b et c sont des terminaux, ne peut pas être décrit par une grammaire non contextuelle. L est fait de phrases comportant deux chaînes de a et b identiques, séparées par un c, comme ababcabab. L'importance de cet exemple provient du fait que L modélise l'obligation, qu'ont la plupart des langages, de vérifier que les identificateurs apparaissant dans les instructions ont bien été préalablement déclarés (la première occurrence de w dans wcw correspond à la déclaration d'un identificateur, la deuxième occurrence de w à l'utilisation de ce dernier).
Autrement dit, l'analyse syntaxique ne permet pas de vérifier que les identificateurs utilisés dans les programmes font l'objet de déclarations préalables. Ce problème doit nécessairement être remis à une phase ultérieure d'analyse sémantique.
III-B. Analyseurs descendants▲
Étant donnée une grammaire G = (VT, VN, S0, P), analyser une chaîne de symboles terminaux w є VT* c'est construire un arbre de dérivation prouvant que S0 ![]() w.
w.
Les grammaires des langages que nous cherchons à analyser ont un ensemble de propriétés qu'on résume en disant que ce sont des grammaires LL(1). Cela signifie qu'on peut en écrire des analyseurs :
- lisant la chaîne source de la gauche vers la droite (gauche = left, c'est le premier L),
- cherchant à construire une dérivation gauche (c'est le deuxième L),
- dans lesquels un seul symbole de la chaîne source est accessible à chaque instant et permet de choisir, lorsque c'est nécessaire, une production parmi plusieurs candidates (c'est le 1 de LL(1)).
À PROPOS DU SYMBOLE ACCESSIBLE. Pour réfléchir au fonctionnement de nos analyseurs il est utile d'imaginer que la chaîne source est écrite sur un ruban défilant derrière une fenêtre, de telle manière qu'un seul symbole est visible à la fois ; voyez la figure 8. Un mécanisme permet de faire avancer - jamais reculer - le ruban, pour rendre visible le symbole suivant.
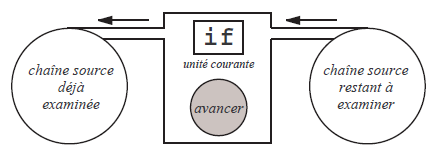
Lorsque nous programmerons effectivement des analyseurs, cette machine à symboles terminaux ne sera rien d'autre que l'analyseur lexical préalablement écrit ; le symbole visible à la fenêtre sera représenté par une variable uniteCourante, et l'opération faire avancer le ruban se traduira par uniteCourante = uniteSuivante() (ou bien, si c'est lex qui a écrit l'analyseur lexical, uniteCourante = yylex()).
III-B-1. Principe▲
ANALYSEUR DESCENDANT. Un analyseur descendant construit l'arbre de dérivation de la racine (le symbole de départ de la grammaire) vers les feuilles (la chaîne de terminaux).
Pour en décrire schématiquement le fonctionnement nous nous donnons une fenêtre à symboles terminaux comme ci-dessus et une pile de symboles, c'est-à-dire une séquence de symboles terminaux et non terminaux à laquelle on ajoute et on enlève des symboles par une même extrémité, en l'occurrence l'extrémité de gauche (c'est une pile couchée à l'horizontale, qui se remplit de la droite vers la gauche).
INITIALISATION. Au départ, la pile contient le symbole de départ de la grammaire et la fenêtre montre le premier symbole terminal de la chaîne d'entrée.
ITÉRATION. Tant que la pile n'est pas vide, répéter les opérations suivantes :
- si le symbole au sommet de la pile (c'est-à-dire le plus à gauche) est un terminal α ;
- si le terminal visible à la fenêtre est le même symbole α, alors :
- dépiler le symbole au sommet de la pile et
- faire avancer le terminal visible à la fenêtre,
- sinon, signaler une erreur (par exemple afficher « α attendu ») ;
- si le terminal visible à la fenêtre est le même symbole α, alors :
- si le symbole au sommet de la pile est un non terminal S ;
- s'il y a une seule production S → S1S2 … Sk ayant S pour membre gauche alors dépiler S et empiler S1S2 … Sk à la place ;
- s'il y a plusieurs productions ayant S pour membre gauche, alors d'après le terminal visible à la fenêtre, sans faire avancer ce dernier, choisir l'unique production S → S1S2 … Sk pouvant convenir, dépiler S et empiler S1S2 … Sk.
TERMINAISON. Lorsque la pile est vide :
- si le terminal visible à la fenêtre est la marque qui indique la fin de la chaîne d'entrée alors l'analyse a réussi : la chaîne appartient au langage engendré par la grammaire ;
- sinon, signaler une erreur (par exemple, afficher « caractères inattendus à la suite d'un texte correct »).
À titre d'exemple, voici la reconnaissance par un tel analyseur du texte « 60 * vitesse + 200 » avec la grammaire G3 de la section 3.1.3Qualités des grammaires en vue des analyseurs :
expression → terme fin expression
fin expression → "+" terme fin expression | ε
terme → facteur fin terme (G3)
fin terme → "*" facteur fin terme | ε
facteur → nombre | identificateur | "(" expression ")"La chaîne d'entrée est donc (nombre « * » identif « + » nombre). Les états successifs de la pile et de la fenêtre sont les suivants :
| fenêtre | pile |
| nombre | expression |
| nombre | terme fin_expression |
| nombre | facteur fin_terme fin_expression |
| nombre | nombre fin_terme fin_expression |
| « * » | fin_terme fin_expression |
| « * » | « * » facteur fin_terme fin_expression |
| identificateur | facteur fin_terme fin_expression |
| identificateur | identificateur fin_temre fin_expression |
| « + » | fin_terme fin_expression |
| « + » | ε fin_expression |
| « + » | fin_expression |
| « + » | « + » terme fin_expression |
| nombre | terme fin_expression |
| nombre | facteur fin_expression |
| nombre | nombre fin_expression |
| ¶ | fin_expression |
| ¶ | ε |
| ¶ |
Lorsque la pile est vide, la fenêtre exhibe ¶, la marque de fin de chaîne. La chaîne donnée appartient donc bien au langage considéré.
III-B-2. Analyseur descendant non récursif▲
Nous ne développerons pas cette voie ici, mais nous pouvons remarquer qu'on peut réaliser des programmes itératifs qui implantent l'algorithme expliqué à la section précédente.
La plus grosse difficulté est le choix d'une production chaque fois qu'il faut dériver un non terminal qui est le membre gauche de plusieurs productions de la grammaire. Comme ce choix ne dépend que du terminal visible à la fenêtre, on peut le faire, et de manière très efficace, à l'aide d'une table à double entrée, appelée table d'analyse, calculée à l'avance, représentant une fonction Choix : VN x VT → P qui à un couple (S, α) formé d'un non terminal (le sommet de la pile) et un terminal (le symbole visible à la fenêtre) associe la production qu'il faut utiliser pour dériver S.
Pour avoir un analyseur descendant non récursif, il suffit alors de se donner une fenêtre à symboles terminaux (c'est-à-dire un analyseur lexical), une pile de symboles comme expliqué à la section précédente, une table d'analyse comme expliqué ici et un petit programme qui implante l'algorithme de la section précédente, dans lequel la partie « choisir la production… » se résume à une consultation de la table P = Choix(S, α).
En définitive, un analyseur descendant est donc un couple formé d'une table dont les valeurs sont intimement liées à la grammaire analysée et d'un programme tout à fait indépendant de cette grammaire.
III-B-3. Analyse par descente récursive▲
À l'opposé du précédent, un analyseur par descente récursive est un type d'analyseur descendant dans lequel le programme de l'analyseur est étroitement lié à la grammaire analysée. Voici les principes de l'écriture d'un tel analyseur :
- Chaque groupe de productions ayant le même membre gauche S donne lieu à une fonction void reconnaitre S(void), ou plus simplement void S(void). Le corps de cette fonction se déduit des membres droits des productions en question, comme expliqué ci-après.
- Lorsque plusieurs productions ont le même membre gauche, le corps de la fonction correspondante est une conditionnelle (instruction if ) ou un aiguillage (instruction switch) qui, d'après le symbole terminal visible à la fenêtre, sélectionne l'exécution des actions correspondant au membre droit de la production pertinente. Dans cette sélection, le symbole visible à la fenêtre n'est pas modifié.
- Une séquence de symboles S1S2 … Sn dans le membre droit d'une production donne lieu, dans la fonction correspondante, à une séquence d'instructions traduisant les actions « reconnaissance de S1 », « reconnaissance de S2 », . . . « reconnaissance de Sn ».
- Si S est un symbole non terminal, l'action « reconnaissance de S » se réduit à l'appel de fonction reconnaitre_S().
- Si α est un symbole terminal, l'action « reconnaissance de α » consiste à considérer le symbole terminal visible à la fenêtre et
- s'il est égal à α, faire passer la fenêtre sur le symbole suivant(27),
- sinon, annoncer une erreur (par exemple, afficher « α attendu »).
L'ensemble des fonctions écrites selon les prescriptions précédentes forme l'analyseur du langage considéré.
L'initialisation de l'analyseur consiste à positionner la fenêtre sur le premier terminal de la chaîne d'entrée.
On lance l'analyse en appelant la fonction associée au symbole de départ de la grammaire. Au retour de cette fonction :
- si la fenêtre à terminaux montre la marque de fin de chaîne, l'analyse a réussi ;
- sinon la chaîne est erronée(28) (on peut par exemple afficher le message « caractères illégaux après une expression correcte »).
Exemple. Voici encore la grammaire G3 de la section 3.1.3Qualités des grammaires en vue des analyseurs :
expression → terme fin expression
fin expression → "+" terme fin expression | ε
terme → facteur fin terme (G3)
fin terme → "*" facteur fin terme | ε
facteur → nombre | identificateur | "(" expression ")"et voici l'analyseur par descente récursive correspondant :
void expression(void) {
terme();
fin_expression();
}
void fin_expression(void) {
if (uniteCourante == '+') {
terminal('+');
terme();
fin_expression();
}
else
/* rien */;
}
void terme(void) {
facteur();
fin_terme();
}
void fin_terme(void) {
if (uniteCourante == '*') {
terminal('*');
facteur();
fin_terme();
}
else
/* rien */;
}
void facteur(void) {
if (uniteCourante == NOMBRE)
terminal(NOMBRE);
else if (uniteCourante == IDENTIFICATEUR)
terminal(IDENTIFICATEUR);
else {
terminal('(');
expression();
terminal(')');
}
}La reconnaissance d'un terminal revient fréquemment dans un analyseur. Nous en avons fait une fonction séparée (on suppose que erreur est une fonction qui affiche un message et termine le programme) :
void terminal(int uniteVoulue) {
if (uniteCourante == uniteVoulue)
lireUnite();
else
switch (uniteVoulue) {
case NOMBRE:
erreur("nombre attendu");
case IDENTIFICATEUR:
erreur("identificateur attendu");
default:
erreur("%c attendu", uniteVoulue);
}
}NOTE. Nous avons écrit le programme précédent en appliquant systématiquement les règles données plus haut, obtenant ainsi un analyseur correct dont la structure reflète la grammaire donnée. Mais il n'est pas interdit de pratiquer ensuite certaines simplifications, ne serait-ce que pour rattraper certaines maladresses de notre démarche. L'appel généralisé de la fonction terminal, notamment, est à l'origine de certains test redondants.
Par exemple, la fonction fin_expression commence par les deux lignes
if (uniteCourante == '+') {
terminal('+');
...si on développe l'appel de terminal, la maladresse de la chose devient évidente
if (uniteCourante == '+') {
if (uniteCourante == '+')
lireUnite();
...Une version plus raisonnable des fonctions fin_expression et facteur serait donc :
void fin_expression(void) {
if (uniteCourante == '+') {
lireUnite();
terme();
fin_expression();
}
else
/* rien */;
}
...
void facteur(void) {
if (uniteCourante == NOMBRE)
lireUnite();
else if (uniteCourante == IDENTIFICATEUR)
lireUnite();
else {
terminal('(');
expression();
terminal(')');
}
}Comme elle est écrite ci-dessus, la fonction facteur aura tendance à faire passer toutes les erreurs par le diagnostic « '(' attendu », ce qui risque de manquer d'à-propos. Une version encore plus raisonnable de cette fonction serait
void facteur(void) {
if (uniteCourante == NOMBRE)
lireUnite();
else if (uniteCourante == IDENTIFICATEUR)
lireUnite();
else if (uniteCourante == '(') {
lireUnite('(');
expression();
terminal(')');
}
else
erreur("nombre, identificateur ou '(' attendus ici");
}III-C. Analyseurs ascendants▲
III-C-1. Principe▲
Comme nous l'avons dit, étant données une grammaire G = {VT, VN, S 0, P} et une chaîne w є VT*, le but de l'analyse syntaxique est la construction d'un arbre de dérivation qui prouve w є L(G). Les méthodes descendantes construisent cet arbre en partant du symbole de départ de la grammaire et en « allant vers » la chaîne de terminaux. Les méthodes ascendantes, au contraire, partent des terminaux qui constituent la chaîne d'entrée et « vont vers » le symbole de départ.
Le principe général des méthodes ascendantes est de maintenir une pile de symboles(29) dans laquelle sont empilés (l'empilement s'appelle ici décalage) les terminaux au fur et à mesure qu'ils sont lus, tant que les symboles au sommet de la pile ne sont pas le membre droit d'une production de la grammaire. Si les k symboles du sommet de la pile constituent le membre droit d'une production alors ils peuvent être dépilés et remplacés par le membre gauche de cette production (cette opération s'appelle réduction). Lorsque dans la pile il n'y a plus que le symbole de départ de la grammaire, si tous les symboles de la chaîne d'entrée ont été lus, l'analyse a réussi.
Le problème majeur de ces méthodes est de faire deux sortes de choix :
- si les symboles au sommet de la pile constituent le membre droit de deux productions distinctes, laquelle utiliser pour effectuer la réduction ?
- lorsque les symboles au sommet de la pile sont le membre droit d'une ou plusieurs productions, faut-il réduire tout de suite, ou bien continuer à décaler, afin de permettre ultérieurement une réduction plus juste ?
À titre d'exemple, avec la grammaire G1 de la section 3.1.1Définitions :
expression → expression "+" terme | terme
terme → terme "*" facteur | facteur (G1)
facteur → nombre | identificateur | "(" expression ")"voici la reconnaissance par un analyseur ascendant du texte d'entrée « 60 * vitesse + 200 », c'est-à-dire la chaîne de terminaux (nombre « * » identificateur « + » nombre) :
| fenêtre | pile | action |
| nombre | décalage | |
| « * » | nombre | réduction |
| « * » | facteur | réduction |
| « * » | terme | décalage |
| identificateur | terme « * » | décalage |
| « + » | terme « * » identificateur | réduction |
| « + » | terme « * » facteur | réduction |
| « + » | terme | réduction |
| « + » | expression | décalage |
| nombre | expression « + » | décalage |
| ¶ | expression « + » nombre | réduction |
| ¶ | expression « + » facteur | réduction |
| ¶ | expression « + » terme | réduction |
| ¶ | expression | succès |
On dit que les méthodes de ce type effectuent une analyse par décalage-réduction. Comme le montre le tableau ci-dessus, le point important est le choix entre réduction et décalage, chaque fois qu'une réduction est possible. Le principe est : les réductions pratiquées réalisent la construction inverse d'une dérivation droite.
Par exemple, les réductions faites dans l'analyse précédente construisent, à l'envers, la dérivation droite suivante :
expression => expression "+" terme
=> expression "+" facteur
=> expression "+" nombre
=> terme "+" nombre
=> terme "*" facteur "+" nombre
=> terme "*" identificateur "+" nombre
=> facteur "*" identificateur "+" nombre
=> nombre "*" identificateur "+" nombreIII-C-2. Analyse LR(k)▲
Il est possible, malgré les apparences, de construire des analyseurs ascendants plus efficaces que les analyseurs descendants, et acceptant une classe de langages plus large que la classe des langages traités par ces derniers.
Le principal inconvénient de ces analyseurs est qu'ils nécessitent des tables qu'il est extrêmement difficile de construire à la main. Heureusement, des outils existent pour les construire automatiquement, à partir de la grammaire du langage ; la section 3.4Yacc, un générateur d'analyseurs syntaxiques présente yacc, un des plus connus de ces outils.
Les analyseurs LR(k) lisent la chaîne d'entrée de la gauche vers la droite (d'où le L), en construisant l'inverse d'une dérivation droite (d'où le R) avec une vue sur la chaîne d'entrée large de k symboles ; lorsqu'on dit simplement LR on sous-entend k = 1, c'est le cas le plus fréquent.
Étant donnée une grammaire G = (VT, VN, S0, P), un analyseur LR est constitué par la donnée d'un ensemble d'états E, d'une fenêtre à symboles terminaux (c'est-à-dire un analyseur lexical), d'une pile de doublets (s, e) où s є E et e є VT et de deux tables Action et Suivant, qui représentent des fonctions :
- Action : E x VT → ({decaler} x E) U({reduire} x P) U { succes; erreur }
- Suivant : E x VN → E
Un analyseur LR comporte enfin un programme, indépendant du langage analysé, qui exécute les opérations suivantes :
Initialisation. Placer la fenêtre sur le premier symbole de la chaîne d'entrée et vider la pile.
Itération. Tant que c'est possible, répéter :
soit s l'état au sommet de la pile et α le terminal visible à la fenêtre
si Action(s, α) = (decaler, s')
empiler (α, s')
placer la fenêtre sur le prochain symbole de la chaîne d'entrée
sinon, si Action(s, α) = (reduire,A → β)
dépiler autant d'éléments de la pile qu'il y a de symboles dans β
(soit (γ, s') le nouveau sommet de la pile)
empiler (A, Suivant(s', A))
sinon, si Action(s, α) = succes
arrêt
sinon
erreur.NOTE. En réalité, notre pile est redondante. Les états de l'analyseur représentent les diverses configurations dans lesquelles la pile peut se trouver, il n'y a donc pas besoin d'empiler les symboles, les états suffisent. Nous avons utilisé une pile de couples (etat, symbole) pour clarifier l'explication.
III-D. Yacc, un générateur d'analyseurs syntaxiques▲
Comme nous l'avons indiqué, les tables Action et Suivant d'un analyseur LR sont difficiles à construire manuellement, mais il existe des outils pour les déduire automatiquement des productions de la grammaire considérée.
Le programme yacc(30) est un tel générateur d'analyseurs syntaxiques. Il prend en entrée un fichier source constitué essentiellement des productions d'une grammaire non contextuelle G, et sort à titre de résultat un programme C qui, une fois compilé, est un analyseur syntaxique pour le langage L(G).
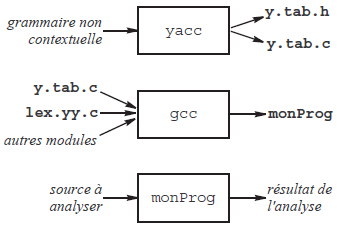
Dans la description de la grammaire donnée à yacc on peut associer des actions sémantiques aux productions ; ce sont des bouts de code source C que yacc place aux bons endroits de l'analyseur construit. Ce dernier peut ainsi exécuter des actions ou produire des informations déduites du texte source, c'est-à-dire devenir un compilateur.
Un analyseur syntaxique requiert pour travailler un analyseur lexical qui lui délivre le flot d'entrée sous forme d'unités lexicales successives. Par défaut, yacc suppose que l'analyseur lexical disponible a été fabriqué par lex.
Autrement dit, sans qu'il faille de déclaration spéciale pour cela, le programme produit par yacc comporte des appels de la fonction yylex aux endroits où l'acquisition d'une unité lexicale est nécessaire.
III-D-1. Structure d'un fichier source pour yacc▲
Un fichier source pour yacc doit avoir un nom terminé par « .y ». Il est fait de trois sections, délimitées par deux lignes réduites au symbole « %% » :
%{
déclarations pour le compilateur C
%}
déclarations pour yacc
%%
règles (productions + actions sémantiques)
%%
fonctions C supplémentairesLes parties « déclarations pour le compilateur C » et « fonctions C supplémentaires » sont simplement recopiées dans le fichier produit, respectivement au début et à la fin de ce fichier. Chacune de ces deux parties peut être absente.
Dans la partie « déclarations pour yacc »on rencontre souvent les déclarations des unités lexicales, sous une forme qui laisse yacc se charger d'inventer des valeurs conventionnelles :
%token NOMBRE IDENTIF VARIABLE TABLEAU FONCTION
%token OU ET EGAL DIFF INFEG SUPEG
%token SI ALORS SINON TANTQUE FAIRE RETOURCes déclarations d'unités lexicales intéressent yacc, qui les utilise, mais aussi lex, qui les manipule en tant que résultats de la fonction yylex. Pour cette raison, yacc produit(31) un fichier supplémentaire, nommé y.tab.h(32), destiné à être inclus dans le source lex (au lieu du fichier que nous avons appelé unitesLexicales.h dans l'exemple de la section 2.3.2Un exemple complet). Par exemple, le fichier produit pour les déclarations ci-dessus ressemble à ceci :
#define NOMBRE 257
#define IDENTIF 258
#define VARIABLE 259
...
#define FAIRE 272
#define RETOUR 273Notez que yacc considère que tout caractère est susceptible de jouer le rôle d'unité lexicale (comme cela a été le cas dans notre exemple de la section 2.3.2Un exemple complet) ; pour cette raison, ces constantes sont numérotées à partir de 256.
SPÉCIFICATION DE VT, VN et S0. Dans un fichier source yacc :
- les caractères simples, encadrés par des apostrophes comme dans les programmes C, et les identificateurs mentionnés dans les déclarations %token sont tenus pour des symboles terminaux ;
- tous les autres identificateurs apparaissant dans les productions sont considérés comme des symboles non terminaux ;
- par défaut, le symbole de départ est le membre gauche de la première règle.
RÈGLES DE TRADUCTION. Une règle de traduction est un ensemble de productions ayant le même membre gauche, chacune associée à une action sémantique.
Une action sémantique (cf. section 3.4.2Actions sémantiques et valeurs des attributs) est un morceau de code source C encadré par des accolades. C'est un code que l'analyseur exécutera lorsque la production correspondante aura été utilisée dans une réduction. Si on écrit un analyseur « pur », c'est-à-dire un analyseur qui ne fait qu'accepter ou rejeter la chaîne d'entrée, alors il n'y a pas d'actions sémantiques et les règles de traduction sont simplement les productions de la grammaire.
Dans les règles de traduction, le métasymbole → est indiqué par deux points « : » et chaque règle (c'est-à-dire chaque groupe de productions avec le même membre gauche) est terminée par un point-virgule « ; ». La barre verticale « | » a la même signification que dans la notation des grammaires.
Par exemple, voici comment la grammaire G1 de la section 3.1.1Définitions :
Expression → expression "+" terme | terme
terme → terme "*" facteur | facteur (G1)
facteur → nombre | identificateur | "(" expression ")"serait écrite dans un fichier source yacc (pour obtenir un analyseur pur, sans actions sémantiques) :
%token nombre identificateur
%%
expression : expression '+' terme | terme ;
terme : terme '*' facteur | facteur ;
facteur : nombre | identificateur | '(' expression ')' ;L'analyseur syntaxique se présente comme une fonction int yyparse(void), qui rend 0 lorsque la chaîne d'entrée est acceptée, une valeur non nulle dans le cas contraire. Pour avoir un analyseur syntaxique autonome, il suffit donc d'ajouter, en troisième section du fichier précédent :
%%
int main(void) {
if (yyparse() == 0)
printf("Texte correct\n");
}En réalité, il faut aussi écrire la fonction appelée en cas d'erreur. C'est une fonction de prototype void yyerror(char *message), elle est appelée par l'analyseur avec un message d'erreur (par défaut « parse error », ce n'est pas très informatif !). Par exemple :
void yyerror(char *message) {
printf(" <<< %s\n", message);
}N.B. L'effet précis de l'instruction ci-dessus, c'est-à-dire la présentation effective des messages d'erreur, dépend de la manière dont l'analyseur lexical écrit les unités lexicales au fur et à mesure de l'analyse.
III-D-2. Actions sémantiques et valeurs des attributs▲
Une action sémantique est une séquence d'instructions C écrite, entre accolades, à droite d'une production.
Cette séquence est recopiée par yacc dans l'analyseur produit, de telle manière qu'elle sera exécutée, pendant l'analyse, lorsque la production correspondante aura été employée pour faire une réduction (cf. « analyse par décalage-réduction » à la section 3.3Analyseurs ascendants).
Voici un exemple simple, mais complet. Le programme suivant lit une expression arithmétique infixée(33) formée de nombres, d'identificateurs et des opérateurs + et *, et écrit la représentation en notation postfixée(34) de la même expression.
%{
#include "syntaxe.tab.h"
extern char nom[]; /* chaîne de caractères partagée avec l'analyseur syntaxique */
%}
chiffre [0-9]
lettre [A-Za-z]
%%
[" "\t\n] { }
{chiffre}+ { yylval = atoi(yytext); return nombre; }
{lettre}({lettre}|{chiffre})* { strcpy(nom, yytext); return identificateur; }
. { return yytext[0]; }
%%
int yywrap(void) {
return 1;
}%{
char nom[256]; /* chaîne de caractères partagée avec l'analyseur lexical */
%}
%token nombre identificateur
%%
expression : expression '+' terme { printf(" +"); }
| terme
;
terme : terme '*' facteur { printf(" *"); }
| facteur
;
facteur : nombre { printf(" %d", yylval); }
| identificateur { printf(" %s", nom); }
| '(' expression ')'
;
%%
void yyerror(char *s) {
printf("<<< \n%s", s);
}
main() {
if (yyparse() == 0)
printf(" Expression correcte\n");
}Construction et essai de cet analyseur :
$ flex lexique.l
$ bison syntaxe.y
$ gcc lex.yy.c syntaxe.tab.c -o rpn
$ rpn
2 + A * 100
2 A 100 * + Expression correcte
$ rpn
2 * A + 100
2 A * 100 + Expression correcte
$ rpn
2 * (A + 100)
2 A 100 + * Expression correcte
$ATTRIBUTS. Un symbole, terminal ou non terminal, peut avoir un attribut, dont la valeur contribue à la caractérisation du symbole. Par exemple, dans les langages qui nous intéressent, la reconnaissance du lexème « 2001 » donne lieu à l'unité lexicale NOMBRE avec l'attribut 2001.
Un analyseur lexical produit par lex transmet les attributs des unités lexicales à un analyseur syntaxique produit par yacc à travers une variable yylval qui, par défaut(35), est de type int. Si vous allez voir le fichier « .tab.h » fabriqué par yacc et destiné à être inclus dans l'analyseur lexical, vous y trouverez, outre les définitions des codes des unités lexicales, les déclarations :
#define YYSTYPE int
...
extern YYSTYPE yylval;Nous avons dit que les actions sémantiques sont des bouts de code C que yacc se borne à recopier dans l'analyseur produit. Ce n'est pas tout à fait exact, dans les actions sémantiques on peut mettre certains symboles bizarres, que yacc remplace par des expressions C correctes. Ainsi, $1, $2, $3, etc. désignent les valeurs des attributs des symboles constituant le membre droit de la production concernée, tandis que $$ désigne la valeur de l'attribut du symbole qui est le membre gauche de cette production.
L'action sémantique { $$ = $1 ; } est implicite et il n'y a pas besoin de l'écrire.
Par exemple, voici notre analyseur précédent, modifié (légèrement) pour en faire un calculateur de bureau effectuant les quatre opérations élémentaires sur des nombres entiers, avec gestion des parenthèses et de la priorité des opérateurs :
Fichier lexique.l : le même que précédemment, à ceci près que les identificateurs ne sont plus reconnus.
%{
void yyerror(char *);
%}
%token nombre
%%
session : session expression '=' { printf("résultat : %d\n", $2); }
|
;
expression : expression '+' terme { $$ = $1 + $3; }
| expression '-' terme { $$ = $1 - $3; }
| terme
;
terme : terme '*' facteur { $$ = $1 * $3; }
| terme '/' facteur { $$ = $1 / $3; }
| facteur
;
facteur : nombre
| '(' expression ')' { $$ = $2; }
;
%%
void yyerror(char *s) {
printf("<<< \n%s", s);
}
main() {
yyparse();
printf("Au revoir!\n");
}Exemple d'utilisation ; ¶ représente la touche « fin de fichier », qui dépend du système utilisé (Ctrl-D, pour UNIX) :
$ go
2 + 3 =
résultat : 5
(2 + 3)*(1002 - 1 - 1) =
résultat : 5000
¶
Au revoir!III-D-3. Conflits et ambiguïtés▲
Voici encore une grammaire équivalente à la précédente, mais plus compacte :
...
%%
session : session expression '=' { printf("résultat: %d\n", $2); }
|
;
expression : expression '+' expression { $$ = $1 + $3; }
| expression '-' expression { $$ = $1 - $3; }
| expression '*' expression { $$ = $1 * $3; }
| expression '/' expression { $$ = $1 / $3; }
| '(' expression ')' { $$ = $2; }
| nombre
;
%%
...Nous avons vu à la section 3.1.3Qualités des grammaires en vue des analyseurs que cette grammaire est ambiguë ; elle provoquera donc des conflits. Lorsqu'il rencontre un conflit(36), yacc applique une règle de résolution par défaut et continue son travail ; à la fin de ce dernier, il indique le nombre total de conflits rencontrés et arbitrairement résolus. Il est impératif de comprendre la cause de ces conflits et il est fortement recommandé d'essayer de les supprimer (par exemple en transformant la grammaire). Les conflits possibles sont :
- Décaler ou réduire ? (« shift/reduce conflict »). Ce conflit se produit lorsque l'algorithme de yacc n'arrive pas à choisir entre décaler et réduire, car les deux actions sont possibles et n'amènent pas l'analyse à une impasse. Un exemple typique de ce conflit a pour origine la grammaire usuelle de l'instruction conditionnelle
| instr_si → si expr alors instr | si expr alors instr sinon instr |
- Le conflit apparaît pendant l'analyse d'une chaîne comme
| si α alors si β alors γ sinon δ |
- lorsque le symbole courant est sinon : au sommet de la pile se trouve alors si β alors γ, et la question est : faut-il réduire ces symboles en instr_si (ce qui revient à associer la partie sinon δau premier si) ou bien faut-il décaler (ce qui provoquera plus tard une réduction revenant à associer la partie sinon δau second si) ?
Résolution par défaut : l'analyseur fait le décalage (c'est un comportement « glouton » : chacun cherche à manger le plus de terminaux possibles). - Comment réduire ? (« reduce/reduce conflict ») Ce conflit se produit lorsque l'algorithme ne peut pas choisir entre deux productions distinctes dont les membres droits permettent tous deux de réduire les symboles au sommet de la pile.
On trouve un exemple typique d'un tel conflit dans les grammaires de langages (il y en a !) où on note avec des parenthèses aussi bien les appels de fonctions que les accès aux tableaux. Sans rentrer dans les détails, il est facile d'imaginer qu'on trouvera dans de telles grammaires des productions complètement différentes avec les mêmes membres droits. Par exemple, la production définissant un appel de fonction et celle définissant un accès à un tableau pourraient ressembler à ceci :
...
appel de fonction → identificateur '(' liste expressions ')'
...
acces tableau → identificateur '(' liste expressions ')'
...La résolution par défaut est : dans l'ordre où les règles sont écrites dans le fichier source pour yacc, on préfère la première production. Comme l'exemple ci-dessus le montre(37), cela ne résout pas souvent bien le problème.
GRAMMAIRES D'OPÉRATEURS. La grammaire précédente, ou du moins sa partie utile, la règle expression, vérifie ceci :
- aucune règle ne contient d'ε-production,
- aucune règle ne contient une production ayant deux non-terminaux consécutifs.
De telles grammaires s'appellent des grammaires d'opérateurs. Nous n'en ferons pas l'étude détaillée ici, mais il se trouve qu'il est très simple de les rendre non ambiguës : il suffit de préciser par ailleurs le sens de l'associativité et la priorité de chaque opérateur.
En yacc, cela se fait par des déclarations %left et %right qui spécifient le sens d'associativité des opérateurs, l'ordre de ces déclarations donnant leur priorité : à chaque nouvelle déclaration, les opérateurs déclarés sont plus prioritaires que les précédents.
Ainsi, la grammaire précédente, présentée comme ci-après, n'est plus ambiguë. On a ajouté des déclarations indiquant que +, -, * et / sont associatifs à gauche(38) et que la priorité de * et / est supérieure à celle de + et -.
%{
void yyerror(char *);
%}
%token nombre
%left '+' '-'
%left '*' '/'
%%
session : session expression '=' { printf("résultat: %d\n", $2); }
|
;
expression : expression '+' expression { $$ = $1 + $3; }
| expression '-' expression { $$ = $1 - $3; }
| expression '*' expression { $$ = $1 * $3; }
| expression '/' expression { $$ = $1 / $3; }
| '(' expression ')' { $$ = $2; }
| nombre
;
%%
...