IV. Analyse sémantique▲
Après l'analyse lexicale et l'analyse syntaxique, l'étape suivante dans la conception d'un compilateur est l'analyse sémantique dont la partie la plus visible est le contrôle de type. Des exemples de tâches liées au contrôle de type sont :
- construire et mémoriser des représentations des types définis par l'utilisateur, lorsque le langage le permet ;
- traiter les déclarations de variables et fonctions et mémoriser les types qui leur sont appliqués ;
- vérifier que toute variable référencée et toute fonction appelée ont bien été préalablement déclarées ;
- vérifier que les paramètres des fonctions ont les types requis ;
- contrôler les types des opérandes des opérations arithmétiques et en déduire le type du résultat ;
- au besoin, insérer dans les expressions les conversions imposées par certaines règles de compatibilité ;
- etc.
Pour fixer les idées, voici une situation typique où le contrôle de type joue. Imaginons qu'un programme, écrit en C, contient l'instruction « i = (200 + j) * 3.14 ». L'analyseur syntaxique construit un arbre abstrait représentant cette expression, comme ceci (pour être tout à fait corrects, à la place de i et j nous aurions dû représenter des renvois à la table des symboles) :
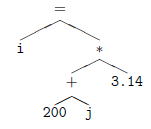
Dans de tels arbres, seules les feuilles (ici i, 200, j et 3.14), ont des types précis(39), tandis que les nœuds internes représentent des opérations abstraites, dont le type exact reste à préciser. Le travail sémantique à faire consiste à « remonter les types », depuis les feuilles vers la racine, rendant concrets les opérateurs et donnant un type précis aux sous-arbres.
Supposons par exemple que i et j aient été déclarées de type entier. L'analyse sémantique de l'arbre précédent permet d'en déduire, successivement :
- que le + est l'addition des entiers, puisque les deux opérandes sont entiers, et donc que le sous-arbre chapeauté par le + représente une valeur de type entier ;
- que le * est la multiplication des flottants, puisqu'un opérande est flottant(40), qu'il y a lieu de convertir l'autre opérande vers le type flottant, et que le sous-arbre chapeauté par * représente un objet de type flottant ;
- que l'affectation qui coiffe l'arbre tout entier consiste donc en l'affectation d'un flottant à un entier, et qu'il faut donc insérer une opération de troncation flottant → entier ; en C, il en découle que l'arbre tout entier représente une valeur du type entier.
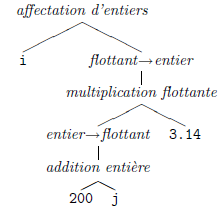
En définitive, le contrôle de type transforme l'arbre précédent en quelque chose qui ressemble à ceci :
IV-A. Représentation et reconnaissance des types▲
Une partie importante du travail sémantique qu'un compilateur fait sur un programme est :
- pendant la compilation des déclarations, construire des représentations des types déclarés dans le programme ;
- pendant la compilation des instructions, reconnaître les types des objets intervenant dans les expressions.
La principale difficulté de ce travail est la complexité des structures à construire et à manipuler. En effet, dans les langages modernes, les types sont définis par des procédés récursifs qu'on peut composer à volonté. Par exemple, en C on peut avoir des entiers, des adresses (ou pointeurs) d'entiers, des fonctions rendant des adresses d'entiers, des adresses de fonctions rendant des adresses d'entiers, des tableaux d'adresses de fonctions rendant des adresses d'entiers, etc. Cela peut aller aussi loin qu'on veut, l'auteur d'un compilateur doit se donner le moyen de représenter ces structures de complexité quelconque.
Faute de temps, nous n'étudierons pas cet aspect des compilateurs dans le cadre de ce cours.
Ainsi, le compilateur que nous réaliserons à titre de projet ne traitera que les types entier et tableau d'entiers.
Pour les curieux, voici néanmoins une suggestion de structures de données pour la représentation des principaux types du langage C dans un compilateur qui serait lui-même(41) écrit en C :
typedef
enum {
tChar, tShort, tInt, tLong, tFloat, tDouble,
tPointeur, tTableau, tFonction, tStructure
} typePossible;
typedef
struct listeDescripteursTypes {
struct descripteurType *info;
struct listeDescripteursTypes *suivant;
} listeDescripteursTypes;
typedef
struct descripteurType {
typePossible classe;
union {
struct {
struct descripteurType *typePointe;
} casPointeur;
struct {
int nombreElements;
struct descripteurType *typeElement;
} casTableau;
struct {
listeDescripteursTypes *typesChamps;
} casStructure;
struct {
listeDescripteursTypes *typesArguments;
struct descripteurType *typeResultat;
} casFonction;
} attributs;
} descripteurType;Ainsi, un type se trouve représenté par une structure à deux champs : classe, dont la valeur est un code conventionnel qui indique de quelle sorte de type il s'agit, et attributs, qui donne les informations nécessaires pour achever de définir le type. Attributs est un champ polymorphe (en C, une union) dont la structure dépend de la valeur du champ classe :
- si la classe est celle d'un type primitif, le champ attributs est sans objet ;
- si le champ classe indique qu'il s'agit d'un type pointeur, alors le champ attributs pointe sur la description du type des objets pointés ;
- si la valeur du champ classe est tTableau alors il faut deux attributs pour définir le type : nombreElements, le nombre de cases du tableau, et typeElement, qui pointe sur la description du type commun des éléments du tableau ;
- s'il s'agit d'un type structure, l'attribut est l'adresse d'une liste chaînée dont chaque maillon contient un pointeur(42) sur un descripteur de type ;
- enfin, si le champ classe indique qu'il s'agit d'un type fonction, alors le champ attribut se compose de l'adresse d'un descripteur de type (le type rendu par la fonction) et l'adresse d'une liste de types (les types des arguments de cette dernière).
On facilite l'allocation dynamique de telles structures en se donnant une fonction :
descripteurType *nouveau(typePossible classe) {
descripteurType *res = malloc(sizeof(descripteurType));
assert(res != NULL);
res->classe = classe;
return res;
}Pour montrer le fonctionnement de cette structure de données, voici un exemple purement démonstratif, la construction « à la main » du descripteur correspondant au type de la variable déclarée, en C, comme suit :
struct {
char *lexeme;
int uniteLexicale;
} motRes[N];La variable est motRes (nous l'avons utilisée à la section 2.2.2Analyseurs lexicaux programmés en dur ), elle est déclarée comme un tableau de N éléments qui sont des structures à deux champs : un pointeur sur un caractère et un entier. Voici le code qui construit un tel descripteur (pointé, à la fin de la construction, par la variable tmp2) :
...
listeDescripteursTypes *pCour, *pSuiv;
descripteurType *pTmp1, *pTmp2;
/* maillon de liste décrivant le type entier */
pCour = malloc(sizeof(listeDescripteursTypes));
pCour->info = nouveau(tInt);
pCour->suiv = NULL;
/* maillon de liste décrivant le type pointeur sur caractère */
pSuiv = pCour;
pCour = malloc(sizeof(listeDescripteursTypes));
pCour->info = nouveau(tPointeur);
pCour->info->attributs.casPointeur.typePointe = nouveau(tChar);
pCour->suiv = pSuiv;
/* pTmp1 va pointer la description de la structure */
pTmp1 = nouveau(tStructure);
pTmp1->attributs.casStructure.typesChamps = pCour;
/* pTmp2 va pointer la description du type tableau */
pTmp2 = nouveau(tTableau);
pTmp2->attributs.casTableau.nombreElements = N;
pTmp2->attributs.casTableau.typeElement = pTmp1;
...Dans le même ordre d'idées, voici la construction manuelle du descripteur du type « matrice de NL x NC flottants » ou, plus précisément, « tableau de NL éléments qui sont des tableaux de NC flottants » (en C, cela s'écrit : float matrice[NL][NC];). À la fin de la construction le descripteur cherché est pointé par pTmp2 :
...
/* description d'une ligne, tableau de NC flottants: */
pTmp1 = nouveau(tTableau);
pTmp1->attributs.casTableau.nombreElements = NC;
pTmp1->attributs.casTableau.typeElement = nouveau(tFloat);
/* description d'une matrice, tableau de NL lignes: */
pTmp2 = nouveau(tTableau);
pTmp2->attributs.casTableau.nombreElements = NL;
pTmp2->attributs.casTableau.typeElement = pTmp1;
...Enfin, pour donner encore un exemple de manipulation de ces structures de données, voici un utilitaire fondamental dans les systèmes de contrôle de type : la fonction booléenne qui fournit la réponse à la question « deux descripteurs donnés décrivent-ils des types identiques ? » :
int memeType(descripteurType *a, descripteurType *b) {
if (a->classe != b->classe)
return 0;
switch (a->classe) {
case tPointeur:
return memeType(a->attributs.casPointeur.typePointe,
b->attributs.casPointeur.typePointe);
case tTableau:
return a->attributs.casTableau.nombreElements ==
b->attributs.casTableau.nombreElements
&& memeType(a->attributs.casTableau.typeElement,
b->attributs.casTableau.typeElement);
case tStructure:
return memeListeTypes(a->attributs.casStructure.typesChamps,
b->attributs.casStructure.typesChamps);
case tFonction:
return memeType(a->attributs.casFonction.typeResultat,
b->attributs.casFonction.typeResultat)
&& memeListeTypes(a->attributs.casFonction.typesArguments,
b->attributs.casFonction.typesArguments);
default:
return 1;
}
}
int memeListeTypes(listeDescripteursTypes *a, listeDescripteursTypes *b) {
while (a != NULL && b != NULL) {
if ( ! memeType(a->info, b->info))
return 0;
a = a->suiv;
b = b->suiv;
}
return a == NULL && b == NULL;
}IV-B. Dictionnaires (tables de symboles)▲
Dans les langages de programmation modernes, les variables et les fonctions doivent être déclarées avant d'être utilisées dans les instructions. Quel que soit le degré de complexité des types supportés par notre compilateur, celui-ci devra gérer une table de symboles, appelée aussi dictionnaire, dans laquelle se trouveront les identificateurs couramment déclarés, chacun associé à certains attributs, comme son type, son adresse(43) et d'autres informations, cf. figure 10.

Nous étudions pour commencer le cahier des charges du dictionnaire, c'est-à-dire les services que le compilateur en attend, puis, dans les sections suivantes, diverses implémentations possibles.
Grosso modo le dictionnaire fonctionne ainsi :
- quand le compilateur trouve un identificateur dans une déclaration, il le cherche dans le dictionnaire en espérant ne pas le trouver (sinon c'est l'erreur « identificateur déjà déclaré »), puis il l'ajoute au dictionnaire avec le type que la déclaration spécifie ;
- quand le compilateur trouve un identificateur dans la partie exécutable(44) d'un programme, il le cherche dans le dictionnaire avec l'espoir de le trouver (sinon c'est l'erreur « identificateur non déclaré »), ensuite il utilise les informations que le dictionnaire associe à l'identificateur.
Nous allons voir que la question est un peu plus compliquée que cela.
IV-B-1. Dictionnaire global & dictionnaire local▲
Dans les langages qui nous intéressent, un programme est essentiellement une collection de fonctions, entre lesquelles se trouvent des déclarations de variables. À l'intérieur des fonctions se trouvent également des déclarations de variables.
Les variables déclarées entre les fonctions et les fonctions elles-mêmes sont des objets globaux. Un objet global est visible(45) depuis sa déclaration jusqu'à la fin du texte source, sauf aux endroits où un objet local de même nom le masque, voir ci-après.
Les variables déclarées à l'intérieur des fonctions sont des objets locaux. Un objet local est visible dans la fonction où il est déclaré, depuis sa déclaration jusqu'à la fin de cette fonction ; il n'est pas visible depuis les autres fonctions. En tout point où il est visible, un objet local masque(46) tout éventuel objet global qui aurait le même nom.
En définitive, quand le compilateur se trouve dans(47) une fonction, il faut posséder deux dictionnaires : un dictionnaire global, contenant les noms des objets globaux couramment déclarés, et un dictionnaire local dans lequel se trouvent les noms des objets locaux couramment déclarés (qui, parfois, masquent des objets dont les noms se trouvent dans le dictionnaire global).
Dans ces conditions, l'utilisation des dictionnaires que fait le compilateur se précise :
- Lorsque le compilateur traite la déclaration d'un identificateur i qui se trouve à l'intérieur d'une fonction, i est recherché dans le dictionnaire local exclusivement ; normalement, il ne s'y trouve pas (sinon, « erreur : identificateur déjà déclaré »). Suite à cette déclaration, i est ajouté au dictionnaire local.
Il n'y a strictement aucun intérêt à savoir si i figure à ce moment-là dans le dictionnaire global. - Lorsque le compilateur traite la déclaration d'un identificateur i en dehors de toute fonction, i est recherché dans le dictionnaire global, qui est le seul dictionnaire existant en ce point ; normalement, il ne s'y trouve pas (sinon, « erreur : identificateur déjà déclaré »). Suite à cette déclaration, i est ajouté au dictionnaire global.
- Lorsque le compilateur compile une instruction exécutable, forcément à l'intérieur d'une fonction, chaque identificateur i rencontré est recherché d'abord dans le dictionnaire local ; s'il ne s'y trouve pas, il est recherché ensuite dans le dictionnaire global (si les deux recherches échouent, « erreur : identificateur non déclaré »). En procédant ainsi on assure le masquage des objets globaux par les objets locaux.
- Lorsque le compilateur quitte une fonction, le dictionnaire local en cours d'utilisation est détruit, puisque les objets locaux ne sont pas visibles à l'extérieur de la fonction. Un dictionnaire local nouveau, vide, est créé lorsque le compilateur entre dans une fonction.
Notez ceci : tout au long d'une compilation le dictionnaire global ne diminue jamais. A l'intérieur d'une fonction il n'augmente pas ; le dictionnaire global n'augmente que lorsque le dictionnaire local n'existe pas.
IV-B-2. Tableau à accès séquentiel▲
L'implémentation la plus simple des dictionnaires consiste en un tableau dans lequel les identificateurs sont placés dans l'ordre où leurs déclarations ont été trouvées dans le texte source. Dans ce tableau, les recherches sont séquentielles. Voyez la figure 11 : lorsqu'il existe, le dictionnaire local se trouve au-dessus du dictionnaire global (en supposant que le tableau grandit du bas vers le haut).
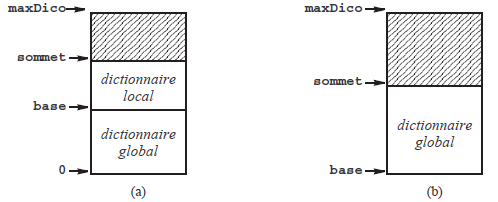
Trois variables sont essentielles dans la gestion du dictionnaire :
- maxDico est le nombre maximum d'entrées possibles (à ce propos, voir « Augmentation de la taille du dictionnaire » un peu plus loin) ;
- sommet est le nombre d'entrées valides dans le dictionnaire ; on doit avoir sommet ≤ maxDico ;
- base est le premier élément du dictionnaire du dessus (c'est-à-dire le dictionnaire local quand il y en a deux, le dictionnaire global quand il n'y en a qu'un).
Avec tout cela, la manipulation du dictionnaire devient très simple. Les opérations nécessaires sont :
- Recherche d'un identificateur pendant le traitement d'une déclaration (que ce soit à l'intérieur d'une fonction ou à l'extérieur de toute fonction) : rechercher l'identificateur dans la portion de tableau comprise entre les bornes sommet - 1 et base ;
- Recherche d'un identificateur pendant le traitement d'une expression exécutable : rechercher l'identificateur en parcourant dans le sens des indices décroissants(48) la portion de tableau comprise entre les bornes sommet - 1 et 0 ;
- Ajout d'une entrée dans le dictionnaire (que ce soit à l'intérieur d'une fonction ou à l'extérieur de toute fonction) : après avoir vérifié que sommet < maxDico, placer la nouvelle entrée à la position sommet, puis faire sommet ← sommet + 1 ;
- Création d'un dictionnaire local, au moment de l'entrée dans une fonction : faire base ← sommet,
- Destruction du dictionnaire local, à la sortie d'une fonction : faire sommet ← base puis base ← 0.
AUGMENTATION DE LA TAILLE DU DICTIONNAIRE. Une question technique assez agaçante qu'il faut régler lors de l'implémentation d'un dictionnaire par un tableau est le choix de la taille à donner à ce tableau, étant entendu qu'on ne connaît pas à l'avance la grosseur (en nombre de déclarations) des programmes que notre compilateur devra traiter.
La bibliothèque C offre un moyen pratique pour résoudre ce problème, la fonction realloc qui permet d'augmenter la taille d'un espace alloué dynamiquement tout en préservant le contenu de cet espace. Voici, à titre d'exemple, la déclaration et les fonctions de gestion d'un dictionnaire réalisé dans un tableau ayant au départ la place pour 50 éléments ; chaque fois que la place manque, le tableau est agrandi d'autant qu'il faut pour loger 25 nouveaux éléments :
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
typedef
struct {
char *identif;
int type;
int adresse;
int complement;
} ENTREE_DICO;
#define TAILLE_INITIALE_DICO 50
#define INCREMENT_TAILLE_DICO 25
ENTREE_DICO *dico;
int maxDico, sommet, base;
void creerDico(void) {
maxDico = TAILLE_INITIALE_DICO;
dico = malloc(maxDico * sizeof(ENTREE_DICO));
if (dico == NULL)
erreurFatale("Erreur interne (pas assez de mémoire)");
sommet = base = 0;
}
void agrandirDico(void) {
maxDico = maxDico + INCREMENT_TAILLE_DICO;
dico = realloc(dico, maxDico);
if (dico == NULL)
erreurFatale("Erreur interne (pas assez de mémoire)");
}
void erreurFatale(char *message) {
fprintf(stderr, "%s\n", message);
exit(-1);
}Pour montrer une utilisation de tout cela, voici la fonction qui ajoute une entrée au dictionnaire :
void ajouterEntree(char *identif, int type, int adresse, int complement) {
if (sommet >= maxDico)
agrandirDico();
dico[sommet].identif = malloc(strlen(identif) + 1);
if (dico[sommet].identif == NULL)
erreurFatale("Erreur interne (pas assez de mémoire)");
strcpy(dico[sommet].identif, identif);
dico[sommet].type = type;
dico[sommet].adresse = adresse;
dico[sommet].complement = complement;
sommet++;
}IV-B-3. Tableau trié et recherche dichotomique▲
L'implémentation des dictionnaires expliquée à la section précédente est facile à mettre en œuvre et suffisante pour des applications simples, mais pas très efficace (la complexité des recherches est, en moyenne, de l'ordre de n/2, soit O(n) ; les insertions se font en temps constant). Dans la pratique on recherche des implémentations plus efficaces, car un compilateur passe beaucoup de temps(49) à rechercher des identificateurs dans les dictionnaires.
Une première amélioration des dictionnaires consiste à maintenir des tableaux ordonnés, permettant des recherches par dichotomie (la complexité d'une recherche devient ainsi O(log2 n), c'est beaucoup mieux). La figure 11 est toujours valable, mais maintenant il faut imaginer que les éléments d'indices allant de base à sommet - 1 et, lorsqu'il y a lieu, ceux d'indices allant de 0 à base - 1, sont placés en ordre croissant des identificateurs.
Dans un tel contexte, voici la fonction existe, qui effectue la recherche de l'identificateur représenté par ident dans la partie du tableau, supposé ordonné, comprise entre les indices inf et sup, bornes incluses. Le résultat de la fonction (1 ou 0, interprétés comme vrai ou faux) est la réponse à la question « l'élément cherché se trouve-t-il dans le tableau ? ». En outre, au retour de la fonction, la variable pointée par ptrPosition contient la position de l'élément recherché, c'est-à-dire :
- si l'identificateur est dans le tableau, l'indice de l'entrée correspondante ;
- si l'identificateur ne se trouve pas dans le tableau, l'indice auquel il faudrait insérer, les cas échéant, une entrée concernant cet identificateur.
int existe(char *identif, int inf, int sup, int *ptrPosition) {
int i, j, k;
i = inf;
j = sup;
while (i <= j) { /* invariant: i <= position <= j + 1 */
k = (i + j) / 2;
if (strcmp(dico[k].identif, identif) < 0)
i = k + 1;
else
j = k - 1;
}
/* ici, de plus, i > j, soit i = j + 1 */
*ptrPosition = i;
return i <= sup && strcmp(dico[i].identif, identif) == 0;
}Voici la fonction qui ajoute une entrée au dictionnaire :
void ajouterEntree(int position, char *identif, int type, int adresse, int complt) {
int i;
if (sommet >= maxDico)
agrandirDico();
for (i = sommet - 1; i >= position; i--)
dico[i + 1] = dico[i];
sommet++;
dico[position].identif = malloc(strlen(identif) + 1);
if (dico[position].identif == NULL)
erreurFatale("Erreur interne (pas assez de mémoire)");
strcpy(dico[position].identif, identif);
dico[position].type = type;
dico[position].adresse = adresse;
dico[position].complement = complt;
}La fonction ajouterEntree utilise un paramètre position dont la valeur provient de la fonction existe. Pour fixer les idées, voici la fonction qui traite la déclaration d'un objet local :
...
int placement;
...
if (existe(lexeme, base, sommet - 1, &placement))
erreurFatale("identificateur déjà déclaré");
else {
ici se place l'obtention des informations type, adresse, complement, etc.
ajouterEntree(placement, lexeme, type, adresse, complement);
}
...Nous constatons que l'utilisation de tableaux triés permet d'optimiser la recherche, dont la complexité passe de O(n) à O(log2 n), mais pénalise les insertions, dont la complexité devient O(n), puisqu'à chaque insertion il faut pousser d'un cran la moitié (en moyenne) des éléments du dictionnaire. Or, pendant la compilation d'un programme il y a beaucoup d'insertions et on ne peut pas négliger a priori le poids des insertions dans le calcul du coût de la gestion des identificateurs.
Il y a cependant une tâche, qui n'est pas la gestion du dictionnaire mais lui est proche, où on peut sans réserve employer un tableau ordonné, c'est la gestion d'une table de mots réservés, comme celle de la section 2.2.2Analyseurs lexicaux programmés en dur . En effet, le compilateur, ou plus précisément l'analyseur lexical, fait de nombreuses recherches dans cette table qui ne subit jamais la moindre insertion.
IV-B-4. Arbre binaire de recherche▲
Cette section suppose la connaissance de la structure de données arbre binaire.
Les arbres binaires de recherche ont les avantages des tables ordonnées, pour ce qui est de l'efficacité de la recherche, sans leurs inconvénients puisque, étant des structures chaînées, l'insertion d'un élément n'oblige pas à pousser ceux qui, d'un point de vue logique, se placent après lui.
Un arbre binaire de recherche, ou ABR, est un arbre binaire étiqueté par des valeurs appartenant à un ensemble ordonné, vérifiant la propriété suivante : pour tout nœud p de l'arbre
- pour tout nœud q appartenant au sous-arbre gauche de p on a q→info ≤ p→info,
- pour tout nœud r appartenant au sous-arbre droit de p on a r→info ≥ p→info.
Voici, par exemple, l'ABR obtenu avec les identificateurs Denis, Fernand, Bernard, André, Gaston, Ernest et Charles, ajoutés à l'arbre successivement et dans cet ordre(50) :
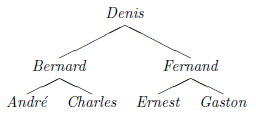
Techniquement, un tel arbre serait réalisé dans un programme comme le montre la figure 12.
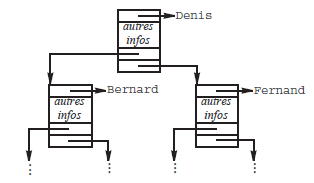
Pour réaliser les dictionnaires par des ABR il faudra donc se donner les déclarations :
typedef
struct noeud {
ENTREE_DICO info;
struct noeud *gauche, *droite;
} NOEUD;
NOEUD *dicoGlobal = NULL, *dicoLocal = NULL;Voici la fonction qui recherche le nœud correspondant à un identificateur donné. Elle rend l'adresse du nœud cherché, ou NULL en cas d'échec de la recherche :
NOEUD *rechercher(char *identif, NOEUD *ptr) {
while (ptr != NULL) {
int c = strcmp(identif, ptr->info.identif);
if (c == 0)
return ptr;
else
if (c < 0)
ptr = ptr->gauche;
else
ptr = ptr->droite;
}
return NULL;
}Cette fonction est utilisée pour rechercher des identificateurs apparaissant dans les parties exécutables des fonctions. Elle sera donc appelée de la manière suivante :
...
p = rechercher(lexeme, dicoLocal);
if (p == NULL) {
p = recherche(lexeme, dicoGlobal);
if (p == NULL)
erreurFatale("identificateur non déclaré");
}
exploitation des informations du nœuds pointé par p
...Pendant la compilation des déclarations, les recherches se font avec la fonction suivante, qui effectue la recherche et, dans la foulée, l'ajout d'un nouveau nœud. Dans cette fonction, la rencontre d'un nœud associé à l'identificateur qu'on cherche est considérée comme une erreur grave. La fonction rend l'adresse du nœud nouvelle créé :
NOEUD *insertion(NOEUD **adrDico, char *identif, int type, int adresse, int complt) {
NOEUD *ptr;
if (*adrDico == NULL)
return *adrDico = nouveauNoeud(identif, type, adresse, complt);
ptr = *adrDico;
for (;;) {
int c = strcmp(identif, ptr->info.identif);
if (c == 0)
erreurFatale("identificateur deja déclaré");
if (c < 0)
if (ptr->gauche != NULL)
ptr = ptr->gauche;
else
return ptr->gauche = nouveauNoeud(identif, type, adresse, complt);
else
if (ptr->droite != NULL)
ptr = ptr->droite;
else
return ptr->droite = nouveauNoeud(identif, type, adresse, complt);
}
}...
p = insertion( &dicoLocal, lexeme, leType, lAdresse, leComplement);
...N.B. Dans la fonction insertion, le pointeur de la racine du dictionnaire dans lequel il faut faire l'insertion est passé par adresse, c'est pourquoi il y a deux ** dans la déclaration NOEUD **adrDico. Cela ne sert qu'à couvrir le cas de la première insertion, lorsque le dictionnaire est vide : le pointeur pointé par adrDico (en pratique il s'agit soit de dicoLocal, soit de dicoGlobal) vaut NULL et doit changer de valeur. C'est beaucoup de travail pour pas grand-chose, on l'éviterait en décidant que les dictionnaires ne sont jamais vides (il suffit de leur créer d'office un nœud bidon sans signification).
RESTITUTION DE L'ESPACE ALLOUÉ. L'implémentation d'un dictionnaire par un ABR possède l'efficacité de la recherche dichotomique, car à chaque comparaison on divise par deux la taille de l'ensemble susceptible de contenir l'élément cherché, sans ses inconvénients, puisque le temps nécessaire pour faire une insertion dans un ABR est négligeable. Hélas, cette méthode a deux défauts :
- la recherche n'est dichotomique que si l'arbre est équilibré, ce qui ne peut être supposé que si les identificateurs sont très nombreux et uniformément répartis ;
- la destruction d'un dictionnaire est une opération beaucoup plus complexe que dans les méthodes qui utilisent un tableau.
La destruction d'un dictionnaire, en l'occurrence le dictionnaire local, doit se faire chaque fois que le compilateur sort d'une fonction. Cela peut se programmer de la manière suivante :
void liberer(NOEUD *dico) {
if (dico != NULL) {
liberer(dico->gauche);
liberer(dico->droite);
free(dico);
}
}Comme on le voit, pour rendre l'espace occupé par un ABR il faut le parcourir entièrement (alors que dans le cas d'un tableau la modification d'un index suffit).
Il y a un moyen de rendre beaucoup plus simple la libération de l'espace occupé par un arbre. Cela consiste à écrire sa propre fonction d'allocation, qu'on utilise à la place malloc, et qui alloue un espace dont on maîtrise la remise à zéro. Par exemple :
#define MAX_ESPACE 1000
NOEUD espace[MAX_ESPACE];
int niveauAllocation = 0;
NOEUD *monAlloc(void) {
if (niveauAllocation >= MAX_ESPACE)
return NULL;
else
return &espace[niveauAllocation++];
}
void toutLiberer(void) {
niveauAllocation = 0;
}IV-B-5. Adressage dispersé▲
Une dernière technique de gestion d'une table de symboles mérite d'être mentionnée ici, car elle est très utilisée dans les compilateurs réels. Cela s'appelle adressage dispersé, ou hash-code(51). Le principe en est assez simple : au lieu de rechercher la position de l'identificateur dans la table, on obtient cette position par un calcul sur les caractères de l'identificateur ; si on s'en tient à des opérations simples, un calcul est certainement plus rapide qu'une recherche.
Soit I l'ensemble des identificateurs existant dans un programme, N la taille de la table d'identificateurs.
L'idéal serait de posséder une fonction h : I → [0,N[ qui serait :
- rapide, facile à calculer ;
- injective, c'est-à-dire qui à deux identificateurs distincts ferait correspondre deux valeurs distinctes.
On ne dispose généralement pas d'une telle fonction car l'ensemble I des identificateurs présents dans le programme n'est pas connu a priori. De plus, la taille de la table n'est souvent pas suffisante pour permettre l'injectivité (qui requiert N ≥ |I|).
On se contente donc d'une fonction h prenant, sur l'ensemble des identificateurs possibles, des valeurs uniformément réparties sur l'intervalle [0,N[. C'est-à-dire que h n'est pas injective, mais :
- si N ≥ |I|, on espère que les couples d'identificateurs i1, i2 tels que i1 ≠ i2 et h(i1) = h(i2) (on appelle cela une collision) sont peu nombreux ;
- si N < |I|, les collisions sont inévitables. Dans ce cas on souhaite qu'elles soient également réparties : pour chaque j є [0,N[ le nombre de i є I tels que h(i) = j est à peu près le même, c'est-à-dire |I|/N . Il est facile de voir pourquoi : h étant la fonction qui place les identificateurs dans la table, il s'agit d'éviter que ces derniers s'amoncellent à certains endroits de la table, tandis qu'à d'autres endroits cette dernière est peu remplie, voire présente des cases vides.
Il est difficile de dire ce qu'est une bonne fonction de hachage. La littérature spécialisée rapporte de nombreuses recettes, mais il n'y a probablement pas de solution universelle, car une fonction de hachage n'est bonne que par rapport à un ensemble d'identificateurs donné. Parmi les conseils qu'on trouve le plus souvent :
- prenez N premier (une des recettes les plus données, mais plus personne ne se donne la peine d'en rappeler la justification) ;
- utilisez des fonctions qui font intervenir tous les caractères des identificateurs ; en effet, dans les programmes on rencontre souvent des grappes de noms, par exemple : poids, poids1, poidsTotal, poids maxi, etc. ; une fonction qui ne ferait intervenir que les cinq premiers caractères ne serait pas très bonne ici ;
- écrivez des fonctions qui donnent comme résultat de grandes valeurs ; lorsque ces valeurs sont ramenées à l'intervalle [0,N[, par exemple par une opération de modulo, les éventuels défauts (dissymétries, accumulations, etc.) de la fonction initiale ont tendance à disparaître.
Une fonction assez souvent utilisée consiste à considérer les caractères d'un identificateur comme les coefficients d'un polynôme P(X) dont on calcule la valeur pour un X donné (ou, ce qui revient au même, à voir un identificateur comme l'écriture d'un nombre dans une certaine base). En C, cela donne la fonction :
int hash(char *ident, int N) {
const int X = 23; /* why not? */
int r = 0;
while (*ident != '\0')
r = X * r + *(ident++);
return r % N;
}Là où les méthodes d'adressage dispersé différent entre elles c'est dans la manière de gérer les collisions.
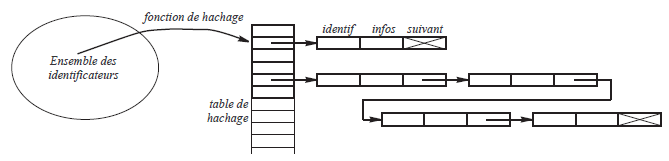
Dans le cas de l'adressage dispersé ouvert, la table qu'on adresse à travers la fonction de hachage n'est pas une table d'identificateurs, mais une table de listes chaînées dont les maillons portent des identificateurs (voyez la figure 13). Si on note T cette table, alors Tj est le pointeur de tête de la liste chaînée dans laquelle sont les identificateurs i tels que h(i) = j.
Vu de cette manière, l'adressage dispersé ouvert apparaît comme une méthode de partitionnement de l'ensemble des identificateurs. Chaque liste chaînée est un compartiment de la partition. Si la fonction h est bien faite, les compartiments ont à peu près la même taille. L'efficacité de la méthode provient alors du fait qu'au lieu de faire une recherche dans une structure de taille |I| on fait un calcul et une recherche dans une structure de taille |I|/N.
Voici la fonction de recherche :
typedef
struct maillon {
char *identif;
autres informations
struct maillon *suivant;
} MAILLON;
#define N 101
MAILLON *table[N];
MAILLON *recherche(char *identif) {
MAILLON *p;
for (p = table[hash(identif, N)]; p != NULL; p = p->suivant)
if (strcmp(identif, p->identif) == 0)
return p;
return NULL;
}et voici la fonction qui se charge de l'insertion d'un identificateur (supposé absent) :
MAILLON *insertion(char *identif) {
int h = hash(identif, N);
return table[h] = nouveauMaillon(identif, table[h]);
}avec une fonction nouveauMaillon définie comme ceci :
MAILLON *nouveauMaillon(char *identif, MAILLON *suivant) {
MAILLON *r = malloc(sizeof(MAILLON));
if (r == NULL)
erreurFatale("Erreur interne (problème d'espace)");
r->identif = malloc(strlen(identif) + 1);
if (r->identif == NULL)
erreurFatale("Erreur interne (problème d'espace)");
strcpy(r->identif, identif);
r->suivant = suivant;
return r;
}